Grunnleggande omgrep og samanhengar. Vinklar

Eit punkt har ein bestemd posisjon, men det har inga utstrekning. Likevel teiknar vi punktet som ein prikk, eit kryss eller liknande, slik at det blir synleg for oss. Det er vanleg å bruke store bokstavar når vi gir namn til punkt.

Ei rett linje, eller berre ei linje, består av uendeleg mange punkt etter kvarandre. Linja har ei uendeleg utstrekning i begge retningar. Ho krummar ikkje. Vi seier at linja har ei uendeleg utstrekning i éin dimensjon. Vi teiknar ei linje som ein tynn strek. Det er vanleg å bruke små bokstavar når vi gir namn til linjer.

Eit linjestykke er ein del av ei linje og er avgrensa av to endepunkt. Vi gir vanlegvis eit linjestykke namn ut frå endepunkta, men det er òg vanleg å bruke små bokstavar som namn.

Linjestykket på biletet er avgrensa av punkta A og B. Vi kan gi linjestykket namnet AB eller til dømes c.

Ein stråle er ein del av ei linje og er avgrensa av eitt endepunkt. Strålen har uendeleg utstrekning i éi retning.

To linjer skjer kvarandre dersom dei har eitt felles punkt.

To linjer som skjer kvarandre, spenner ut eit plan. Eit plan har uendeleg utstrekning i to dimensjonar. Vi kan tenke på eit ark som eit utsnitt av eit plan.

I plangeometrien studerer vi linjer og punkt i eitt og same plan.

To linjer i eit plan har anten eitt eller ingen punkt felles. Dersom linjene ikkje har eitt felles punkt, er dei parallelle.

Når to linjer a og b er parallelle, skriv vi a||b.

Ein vinkel fortel korleis to linjer ligg i forhold til kvarandre. I samanheng med vinklar ser vi òg på omgrep som toppvinklar og samsvarande vinklar.

Vinkel

Når to strålar har felles startpunkt, dannar dei ein vinkel. Det felles startpunktet kallar vi for toppunktet til vinkelen. Strålane kallar vi for vinkelbein. Sjå den første figuren. Sett frå toppunktet får vi høgre vinkelbein og venstre vinkelbein.

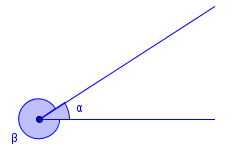
To strålar med felles startpunkt dannar eigentleg to vinklar. Sjå den andre figuren. Når vi snakkar om vinkelen mellom to strålar, meiner vi vanlegvis den minste vinkelen, kalla α (alfa) på figuren.

Vinkelmål

Det er vanleg å dele omkrinsen til sirkelen i 360 delar, eller gradar. Måling av vinklar bygger på denne inndelinga.

Vi tenker oss at vi plasserer ein sirkel med sentrum i toppunktet til ein vinkel.

Ein vinkel som spenner over halvparten av omkrinsen til sirkelen, er 180°.

🤔 Tenk over: Dersom vinkelen α på figuren over er 50°, kor stor er vinkelen β (beta)?

Ein vinkel som spenner over ein fjerdedel av omkrinsen til sirkelen, er $$ \frac{360°}{4}=90°$$. Denne vinkelen kallar vi ein rett vinkel. Vi markerer at ein vinkel er rett, ved å erstatte vinkelbogen med to rette linjer, slik figuren viser.

Med utgangspunkt i den rette vinkelen definerer vi desse vinkeltypane:

• Ein vinkel mellom 0° og 90° kallar vi ein spiss vinkel.

• Ein vinkel mellom 90° og 180° kallar vi ein stump vinkel.

• To vinklar som til saman er 90°, kallar vi komplementvinklar.

• To vinklar som til saman er 180°, kallar vi supplementvinklar.

Namnsetjing av vinklar

Ofte bruker vi greske bokstavar til å setje namn på vinklar, slik vi har gjort øvst på sida. Dersom det ligg namngitte punkt på vinkelbeina, slik som B og C på figuren her, kan vi bruke punkta inkludert toppunktet A til å setje nytt namn på vinkel α.

Vi tenker oss at vi står i toppunktet A og ser mot vinkelbogen til α. Vi bruker namnet på eit punkt på det høgre vinkelbeinet først (B), namnet på toppunktet til vinkelen i midten og namnet på eit punkt på det venstre vinkelbeinet sist (C). På figuren kan vi derfor kalle vinkelen α for BAC. Ei namnsetjing ut frå punkt kan gjere det lettare å identifisere vinklar i meir kompliserte figurar.

Merk at vi må ha regelen om høgre vinkelbein først, elles veit vi ikkje om vi meiner den spisse vinkelen α på figuren eller vinkelen β, han som utgjer resten av ein hel sirkel saman med α.

🤔 Tenk over: Kva skal vi kalle vinkel β dersom vi skal setje namn på vinkelen ut ifrå namna på punkta?

Dersom vi har ein enkel figur med namngitte hjørne, til dømes ein trekant ABC, er det òg vanleg å namngi vinkelen med berre toppunktet.

Normalar

Figuren viser to linjer a og b som dannar ein vinkel på 90 gradar med kvarandre. Vi seier òg at linjene står vinkelrett på kvarandre.

Vi seier at to linjer a og b som står vinkelrett på kvarandre, står normalt på hverandre. Vi kan òg seie at a er ein normal til b.

Matematisk skriv vi $a\perp b$.

Toppvinklar

Nå to linjer skjer kvarandre, er to og to av dei fire vinklane som blir danna, alltid like store. Vi kan bevise det på denne måten:

På figuren er v og w supplementvinklar. Det betyr at

$$ \begin{array}{rcl}v+w& = & 180°\\ v& =& 180°-w\end{array}$$

Vi har òg at

$$ \begin{array}{rcl}u+w& = & 180°\\ u& =& 180°-w\end{array}$$

Det må bety at $u=v$ .

Det same resonnement gir at $w=z$ .

Samsvarande vinklar

Figuren viser to ikkje-parallelle linjer m og n som begge blir skorne av ei tredje linje l. Vinklane α og β kallar vi samsvarande vinklar sidan overskjeringslinja l er venstre vinkelbein i begge vinklane. Vinklane γ (gamma) og δ (delta) er eit anna par av samsvarande vinklar sidan overskjeringslinja l er venstre vinkelbein òg i desse to vinklane.

🤔 Tenk over: Er vinklane α og β like store?

Samsvarande vinklar ved parallelle linjer

På figuren er α og β samsvarande vinklar fordi venstre vinkelbein er felles
(linja l) etter definisjonen over. Forskjellen på figuren her og figuren lenger opp er at i tillegg er høgre vinkelbein i vinklane, linjene m og n, parallelle.

🤔 Tenk over: Er vinklane α og β like store no?

Vi har derfor følgande setning:

Når vinkelbein står parvis normalt på kvarandre

På figuren har vi at det venstre vinkelbeinet til vinkel u, linjestykket DE, står normalt på det venstre vinkelbeinet til vinkel v, linjestykket AC.

🤔 Bruk figuren og tenk over: Gjeld dette det høgre vinkelbeinet for dei to vinklane òg?

Vi kan bruke dette saman med det vi veit om toppvinklar til å forklare kvifor vinklane u og v er like.

• Vinkel u er ein av dei andre vinklane i den rettvinkla trekanten ABC. Tilsvarande er vinkel v ein av dei andre vinklane i den rettvinkla trekanten CDE.

• Dei to trekantane har eitt hjørne felles: C. Det betyr at vinklane i dette hjørnet er like for dei to trekantane fordi vinklane er toppvinklar.

• Sidan to og to av vinklane i dei to trekantane er like, er trekantane formlike, og vinklane u og v må òg vere like.

Dette gir følgande nyttige setning: