Tiarpotensar og tal på standardform

Vi bruker ofte potensar med grunntalet 10 når vi reknar med svært store tal eller svært små tal. Tabellen nedanfor viser tiarpotensar av ulik storleik. Desse har eigne namn (prefiks). Ein del av desse bør du kunne.

Eit oversyn over nokre prefiks til tiarpotensar:

Marknadsverdien av oljefondet kan det vere interessant å følgje med på. Hausten 2020 kunne denne verdien variere mellom 10 680 milliardar kroner og 10 710 milliardar kroner i løpet av berre fem minutt.

Det er ikkje noko poeng for oss å vite på kronenivå kva verdien er. Det held for oss å runde av verdien til cirka 11 000 milliardar kroner.

Det er òg greitt å skrive tal berre med talsiffer. Til dømes har ordet billion ulik betydning i Noreg og i USA. 11 000 milliardar kroner blir då 11 000 000 000 000 kroner. Det blir svært mange siffer å halde styr på.

11 000 000 000 000 kan òg skrivast som $$ 1,1·{10}^{13}$$. Då har vi skrive talet på standardform.

Definisjon av standardform

Eit tal er skrive på standardform når vi skriv det som eit tal frå 1 til 10 multiplisert med ein potens av 10 der eksponenten er eit heilt tal.

Kvifor og korleis vi kan skrive tal på standardform

Vi ser på talet 2 357. Talsystemet vårt er eit posisjonssystem. Det vil seie at det er det enkelte sifferet si plassering som bestemmer verdien av sifferet.

$\begin{array}{ccccccc}& & & 2 & 0& 0& 0\\ & & & & 3& 0& 0\\ & & & & & 5& 0\\ & +& & & & & 7\\ & =& & 2& 3& 5& 7\\ & & & & & & \end{array}$

Det første sifferet, 2, har verdien 2 000. Det neste, 3, har verdien 300. Sifferet 5 har verdien 50, mens det siste sifferet, 7, fortel at vi har 7 einarar. Det første sifferet gir altså talet på 1 000, det neste talet på 100, det tredje talet på tiarar og det siste talet på einarar.

Vi kan setje eit kommateikn etter sifferet 7. Då vil eventuelle siffer etter 7 gi talet på tidelar, hundredelar og så vidare, avhengig av posisjonen til sifferet.

Kommateiknet fortel altså kor vi byrjar å telje einarar.

Vi kan flytte kommaet ein plass til venstre og skrive $235,7$. Då er verdien av alle siffer blitt dividert med 10. Sifferet 3 har ikkje lenger verdien 300, men har no verdien 30. Talet $235,7$ kan få tilbake verdien sin som 2 357 ved at vi multipliserer det med 10.

Vi kan halde fram slik:

$\begin{array}{rcl}& & \begin{array}{rcl}2357& = & 2357·{10}^0\\ & & \\ 2357& =& 235,7·{10}^1\\ & & \\ 2357& =& 23,57·{10}^2\\ & & \\ 2357& =& 2,357·{10}^3\end{array}\end{array}$

I den siste linja har vi skrive talet 2 357 som eit tal mellom 1 og 10 multiplisert med ein tiarpotens. Vi seier då at vi har skrive talet på standardform.

I byrjinga av 2011 var folketalet i verda cirka 6 894 000 000.

Dette talet kan vi skrive på standardform som

$6 894 000 000=6,894·{10}^9\approx 6,9·{10}^9$

Ovanfor har vi runda av til éin desimal i desimaldelen av talet. Vi må då hugse på dei reglane som gjeld for avrunding.

Avrunding

Små tal på standardform

Vi ser på talet $0,023$. Hugs igjen at talsystemet vårt er eit posisjonssystem. Kommateiknet fortel kor vi byrjar å telje einarar. Den første plassen etter kommaet er tidelsplassen som fortel kor mange tidelar vi har. Vi har i eksempelet vårt 0 tidelar. Den andre plassen angir hundredelar. Vi har 2 hundredelar, og siste siffer fortel at vi har 3 tusendelar.

$\begin{array}{rcl}0,02& = & \frac{2}{100}\\ & & \\ 0,003& =& \frac{3}{1000}\end{array}$

Vi kan flytte kommaet ein plass til høgre, og skrive $0,23$. Då har verdien av alle siffer blitt multiplisert med 10. Sifferet 2 har ikkje lenger verdien 2 hundredelar, men har no verdien 2 tidelar. For at talet skal få tilbake den opphavlege verdien sin, må vi dividere heile talet med 10. Det er det same som å multiplisere det med ${10}^{-1}$. Talet $2,3$ kan få tilbake verdien sin som $0,023$ ved at vi dividerer det med 100.

$\begin{array}{rcl}& & \begin{array}{rcl}0,023& = & 0,023·{10}^0\\ & & \\ 0,023& =& 0,23·{10}^{-1}\\ & & \\ 0,023& =& 2,3·{10}^{-2}\end{array}\end{array}$

I den siste linja har vi skrive talet $0,023$ som eit tal mellom 1 og 10 multiplisert med ein tiarpotens. Vi har skrive talet på standardform.

Vatn er bygd opp av vassmolekyl. Massen av eitt vassmolekyl er

$\begin{array}{rcl}& & \begin{array}{rcl}m& = & 0,0000000000000000000000000299 \mathrm{kg}\\ & & \\ & =& 2,99·{10}^{-26} \mathrm{kg}\end{array}\end{array}$.

Her ser du at det er føremålstenleg å bruke standardform.

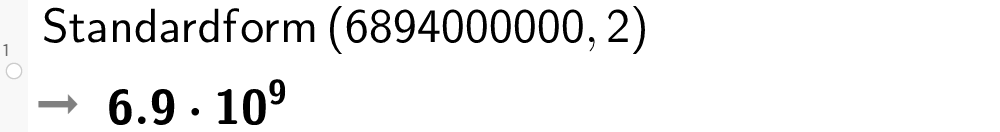
I GeoGebra bruker vi vi kommandoen "Standardform(<Tal>)" eller "Standardform(<Tal>,<Gjeldande siffer>)" for å skrive eit tal eller rekneuttrykk på standardform.

I GeoGebra bruker vi òg bokstaven E for tiarpotens.