Fagartikkel
Volum og overflate av sylinder
Vi har greie formlar for volum og overflate av sylindrar.
Figuren til høgre viser ein sylinder. Grunnflata er ein sirkel, og sylinderen er rett når høgda frå sentrum i toppflata treffer sentrum i grunnflata.
Her er også volumet lik . Det tyder at
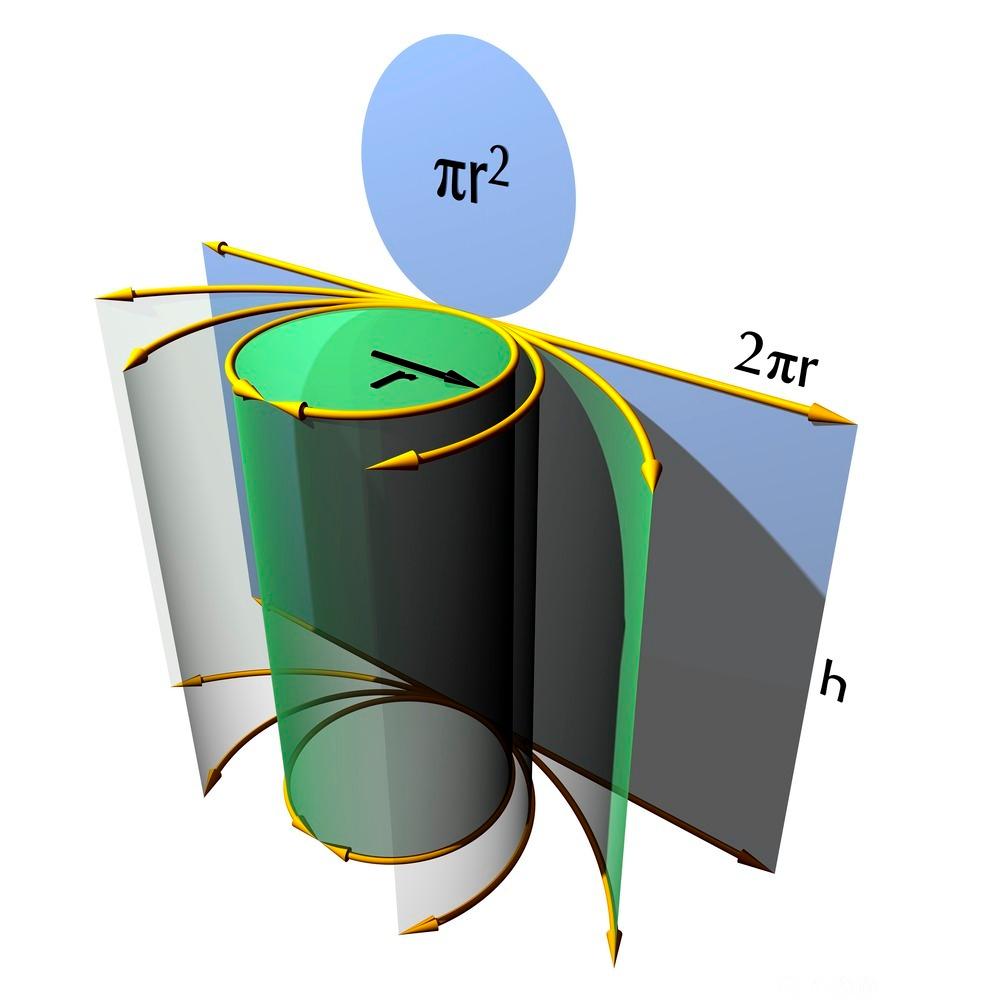
For å finne overflata må vi tenkje oss sylinderen klipt opp og bretta ut slik teikninga nedanfor viser. Topp og botn gir to sirklar, og sideflata gir eit rektangel med grunnlinje lik omkrinsen av sirklane.
Formlar for volum og overflateareal av ein sylinder med høgd og som radius i grunnflata.
I ein sylinderforma kakeboks er diameteren i grunnflata
og høgda .

Volumet blir
Overflata består av topp og botn som er sirkelforma og ei rektangulær sideflate.
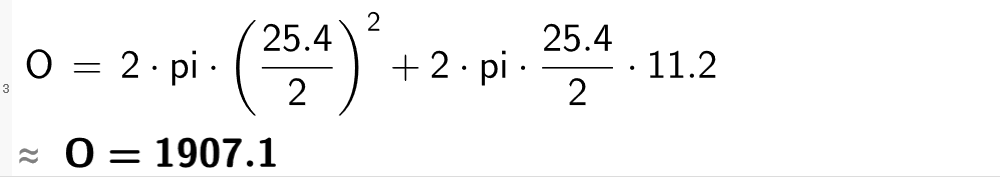
Arealet til overflata blir