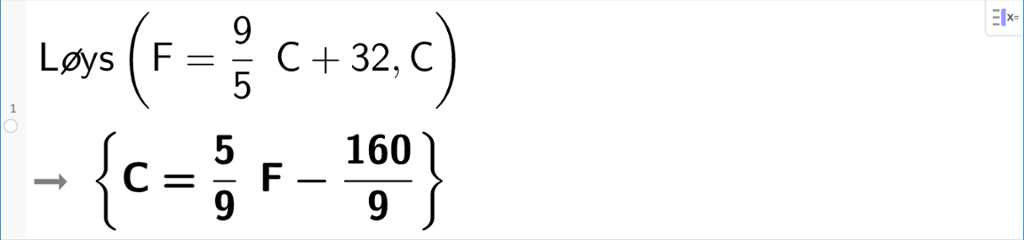Formelrekning
Heimebanen til Liverpool FC heiter Anfield Stadium, eller berre Anfield. Banestorleiken er 100 meter x 69 meter.
a) Kva slags geometrisk figur er ein fotballbane? Skriv opp formelen vi bruker for å rekne ut arealet av ein slik figur.
b) Kor mange kvadratmeter er Anfield?
Old Trafford er heimebanen til Manchester United. Banestorleiken er 106 meter x 69 meter.
c) Kor mange kvadratmeter større er banen til Manchester United enn banen til Liverpool FC?
Grunnflata til ein normalt stor einebustad er 100 m2.
d) Kor mange einebustader av denne storleiken er det plass til på kvart av stadiona?
Ellen hadde på 2000-tallet eit såkalla kontantkort på mobilen. Det kosta 0,59 kr for ei tekstmelding. La A stå for talet på tekstmeldingar og x for kor mye pengar det er på kontantkortet.
a) Finn ein formel for talet på meldingar ho kan sende for pengane som er på kortet.
b) Kor mange tekstmeldingar kan Ellen sende dersom ho har 150 kr igjen på kontantkortet?
Løys oppgåvene utan hjelpemiddel.
Gitt formelen
a) farten, v
b) tida, t
Løys oppgåvene utan hjelpemiddel.
a) Arealet av ein sirkel er gitt ved formelen
Løys formelen med omsyn på r.
b) Volumet av ein terning er gitt ved fomelen
Løys formelen med omsyn på s.
c) Volumet av ein sylinder er gitt ved
1) Løys formelen med omsyn på h.
2) Løys formelen med omsyn på r.
d) Volumet av ei kjegle er gitt ved
1) Løys formelen med omsyn på h.
2) Løys formelen med omsyn på r.
e) Volumet av ei kule er gitt ved
Løys formelen med omsyn på r.
Løys oppgåvene utan hjelpemiddel.
Frå fysikken har vi desse formlane.
Løys formlane med omsyn på t.
a)
b)
c)
Løys oppgåvene med hjelpemiddel.
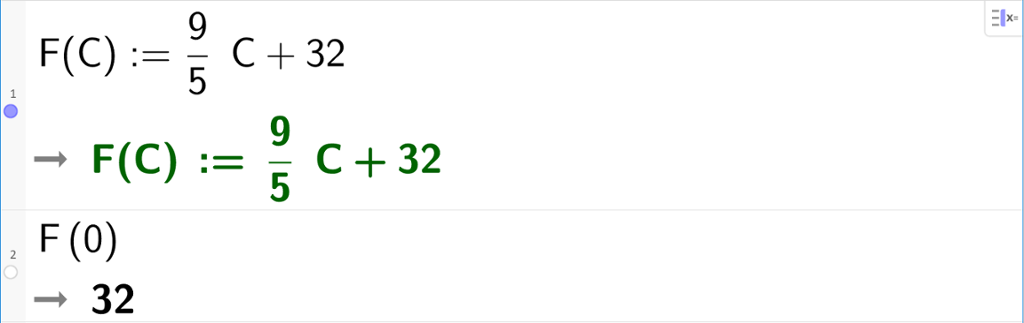
Samanhengen mellom fahrenheitgrader og celsiusgrader er gitt ved formelen
Her står C for temperaturen målt i celsiusgrader og F for temperaturen målt i fahrenheitgrader.
a) Gradestokken viser ein dag 0°C. Kor mange grader fahrenheit svarar dette til?
b) Løys formelen med omsyn på C.
c) Gradestokken viser 65°F. Kor mange grader celsius svarar dette til?
Løys oppgåvene med hjelpemiddel.
Eit telefonabonnement kosta i 2008 49 kroner i fast månadspris og 0,85 kroner per minutt for samtaler. Eit anna abonnement kosta 99 kroner i fast månadspris og 0,59 kroner per minutt for samtaler.
Ved kor mange minutt ringjetid er dei to abonnementa likeverdige i pris?
Løys oppgåvene utan hjelpemiddel.
Vinkelsummen i ein trekant er 180°, i ein firkant 360°, og i ein femkant 540° .
a) Lag ein formel som viser vinkelsummen V i en mangekant med n sider.
I ein regulær mangekant er vinklane like store, til dømes er vinklane i ein regulær trekant 60°, i ein regulær firkant 90° og i ein regulær femkant 108°.
b) Finn ein formel som viser vinkelen i ein regulær n-kant.
Kva kan du om formelrekning?
Filer
- Formelregning(DOCX)
- Formelregning(PDF)