Bokstavrekning
Arealet av eit rektangel
Figuren viser eit rektangel med grunnlinje g og høgde h. Formelen for å rekne ut arealet av eit rektangel er
Du må altså multiplisere (gonge) grunnlinja med høgda for å rekne ut arealet.
Døme
Vi skal rekne ut arealet til ein fotballbane der sidelengdene er 68 m og 105 m.
Ein fotballbane er rektangelforma. Vi lar den lengste sida vere grunnlinja og den kortaste sida vere høgda.

Vi får at
Bokstavane i formelen representerer tal, og ein formel er ei oppskrift for korleis vi skal rekne ut ein storleik ved å erstatte bokstavane med tal. Når vi kjenner grunnlinja og høgda, kan vi rekne ut storleiken arealet.
I mange tilfelle er det lurt å rekne med bokstavar i staden for tal. Dette kallar vi algebra.
Reknereglane vi bruker når vi reknar med bokstavar, er akkurat dei same som gjeld for rekning med tal. Dersom du lurer på om du har rekna rett, kan du erstatte bokstavane med tal og sjå om utrekninga gir same svar.
Bokstavar og programmering
Vi kan lage eit program som reknar ut arealet av rektangel for oss. Når vi programmerer, lar vi ofte bokstavar, eller variablar, representere tal vi skal rekne med. Til dømes kan vi i programmet lage ein variabel h, la han stå for høgda i eit rektangel og gi han verdien 68. I programmeringsspråket Python ville vi då ha skrive
h = 68
Så kan vi lage ein variabel "g" for grunnlinja i rektangelet og sette han til verdien 105 på tilsvarande måte. Til slutt kan vi be programmet rekne ut arealet ved å skrive
g·h
i programmet.
Dette kan du lese meir om på teorisida "Variabler, matematiske operatorer og kommandoen print()".
Vi kan rekne med bokstavar utan å setje inn tal for dei, men vi må hugse at bokstavar står for tal. Det vil seie at vi må rekne med bokstavar som om dei var tal. Vi skal no sjå på nokre reglar som forenklar rekninga med bokstavar.
1. Vi sløyfar multiplikasjonsteiknet mellom eit tal og ein bokstav
Når vi skriv produktet mellom to tal, til dømes
Når vi erstattar 3-talet med ein bokstav og får til dømes
2. Vi kan forenkle uttrykk ved å addere og subtrahere like ledd
Vi tek for oss dette reknestykket:
Sidan både 2 og 3 skal gongast med 4, kan vi like gjerne rekne slik:
Dersom vi no erstattar talet 4 med bokstaven
Dette betyr at vi kan forenkle uttrykk ved å addere (legge saman) og subtrahere (trekke frå) like ledd. Til dømes kan det følgande uttrykket forenklast slik:
3. Vi forkortar brøkar ved å dividere med same faktor i teljar og nemnar
Når vi skal forkorte brøkar, kan det vere lurt å faktorisere først. Til dømes kan vi faktorisere talet 6 til
Vi kan forenkle brøkar ved først å faktorisere og så dividere (dele) med dei same faktorane i teljaren og i nemnaren (vi "stryk" faktor mot faktor):
Dersom vi no erstattar talet 3 med bokstaven
4. Vi kan løyse opp (fjerne) parentesar
Vi tek for oss dette reknestykket med tal:
Frå reglane om reknerekkefølge har vi at det som står inni parentesar, alltid skal reknast ut først. Vi får derfor at
Men følgande måte å rekne på gir det same resultatet:
Hugs at forteiknet til 3-talet og 4-talet inni parentesane eigentleg er "+" (pluss) sidan det ikkje står noko forteikn. Med forteikn blir reknestykket slik:
Det viser seg at denne måten å rekne på alltid blir riktig.
Ein parentes, inkludert rekneteiknet pluss framfor parentesen, kan fjernast ved at vi beheld alle ledda inni parentesen og oppfattar plussteikn og minusteikn som rekneteikn.
Ein parentes, inkludert rekneteiknet minus framfor parentesen, kan fjernast ved at vi skiftar teikna framfor alle ledda inni parentesen og oppfattar desse som rekneteikn.
Du kan lese om forskjellen på rekneteikn og forteikn på teorisida "Rekneartar og negative tal".
5. Vi kan multiplisere tal med parentesuttrykk
Vi tek for oss reknestykket
Sidan det som står inni parentesen, skal reknast ut først, får vi at
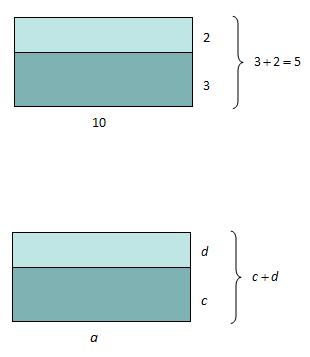
Vi kan tolke dette geometrisk som arealet av heile det store rektangelet til høgre med grunnlinje 10 og høgde 5.
Dette arealet kan vi òg sjå på som summen av areala til dei to små rektangla. Desse er
Det betyr at
Vi erstattar tala i reknestykket ovanfor med bokstavar. Den same geometriske tolkinga på figuren til høgre som på figuren ovanfor gir at
Generelt kan vi seie at når vi multipliserer eit tal med eit parentesuttrykk, må vi multiplisere talet med alle ledda inni parentesen.
Døme
6. Vi kan multiplisere to parentesuttrykk med kvarandre
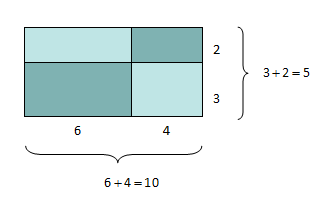
Vi tek for oss reknestykket
Sidan det som står inni parentesen skal reknast ut først, får vi at
Geometrisk kan vi tolke dette som arealet av heile det store rektangelet ovanfor med grunnlinje 10 og høgde 5.
Men vi ser geometrisk at vi kan sjå på dette arealet som summen av areala av fire mindre rektangel. Desse areala er høvesvis
Det betyr at
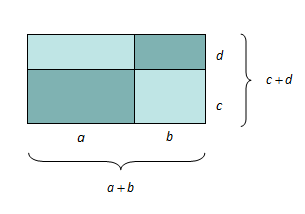
Vi erstattar tala i reknestykket ovanfor med bokstavar. Den same geometriske tolkinga på figuren til høgre som på figuren ovanfor gir at
Generelt kan vi seie at når vi multipliserer to parentesuttrykk med kvarandre, må vi multiplisere kvart ledd i den eine parentesen med kvart ledd i den andre parentesen, slik:
Døme
Kjem