Arealformlar
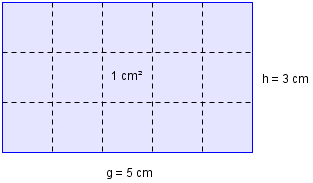
I eit rektangel som er cm langt og cm høgt kan vi få plass til kvadrat som kvar har eit areal på cm2. Det tyder at arealet er på cm2.
Vi kan altså finne arealet til eit rektangel ved å multiplisere grunnlinja med høgda, eller det vi ofte kaller lengd med bredde.
Vi får ein formel for arealet til eit rektangel
Hugs at sidene må ha same måleeining når vi skal rekne ut arealet.
På figuren til høgre kan du samanlikne arealet av rektangelet med grunnlinje og høgd med arealet av trekanten med grunnlinje og høgd .
Du vil sannsynlegvis bli overtydd om at arealet av rektangelet er dobbelt så stort som arealet av trekanten.
Sidan arealet av rektangelet kan finnast ved å multiplisere grunnlinja med høgda, , så er arealet av trekanten
Du kan no ta for deg eit parallellogram, ein rombe og eit trapes, og sjå om du kan lage arealformlar for desse figurane på same måte som for trekantar. Du kan samanlikne dine formlar med formlane i skjemaet nedanfor.
Namn | Arealformel |
|---|---|
Kvadrat | |
Rektangel | |
Trekant | |
Parallellogram | |
Rombe | |
Trapes | |
Sirkel |
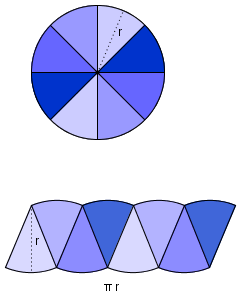
Det er ikkje så lett å gjere ein sirkel om til eit rektangel og på den måten finne formelen for arealet. Vi får likevel ei brukbar tilnærming ved metoden vist i figuren.
Vi deler sirkelen inn i like sektorar. Så stiller vi sektorane annankvar opp og ned, slik at sektorane tilnærma blir eit parallellogram med grunnlinje tilnærma lik
Jo fleire sektorar vi deler sirkelen inn i, jo betre blir tilnærminga. Dersom vi deler sirkelen i veldig mange sektorar, får vi tilnærma eit rektangel.