Smittespreiing – modellar
Dei fleste land kom fram til at drastiske tiltak måtte setjast i verk, sjølv om det betydde store endringar i kvardagen til innbyggarane. For å hindre smittespreiing vart alle offentlege og private bedrifter stengde ned, og kommunikasjon mellom menneske måtte gå føre seg over nettet. Noreg var eit av desse landa.

Andre land valde ein annan strategi og lét smitten spreie seg meir eller mindre ukontrollert utan store inngrep, i håp om at flokkimmunitet ville stoppe spreiinga på ein effektiv måte. Sverige var eit av desse.
Kva er den beste løysinga?
Vala dei ulike landa tok, baserte seg på råd frå ekspertar innan smittespreiing og på ny kunnskap om sjølve viruset. Men andre omsyn vart òg tekne med i vurderinga. Det var spesielt påverknaden på samfunnsøkonomien som vart drøfta. Uansett kva løysingar som vart valde, medførte dei både fordelar og ulemper.
Stengde samfunn

Fordelane ved å stenge ned samfunnet er at få menneske blir smitta, helsevesenet har nok kapasitet, og det blir få dødsfall. Ulempene er bedrifter som slit, mange permitterte, heimeskule, minimal sosial omgang og at størstedelen av befolkninga framleis er sårbare for smitte. For at denne strategien skal verke på sikt, må det utviklast vaksinar. Menneske som er vaksinerte, vil vere beskytta mot dette viruset, og dei smittar heller ikkje andre.
Flokkimmunitet gjennom sjukdom eller vaksine
Dei som har vore gjennom ein covid-19-infeksjon, opparbeider immunitet som beskyttar mot ny smitte av dette viruset så lenge immuniteten varer, på same måte som vaksinen mot same virus verkar. Viss mange menneske får sjukdommen og blir immune, vil befolkninga oppnå flokkimmunitet. Ulempa er at nokre blir svært sjuke og mange døyr.
To andre moment vi må ta med i vurderinga, er at immunitet kan ha avgrensa varigheit, og at virus muterer hyppig. Dei som har oppnådd immunitet gjennom sjukdom eller gjennom vaksinasjon, kan bli utsette for ny smitte seinare.
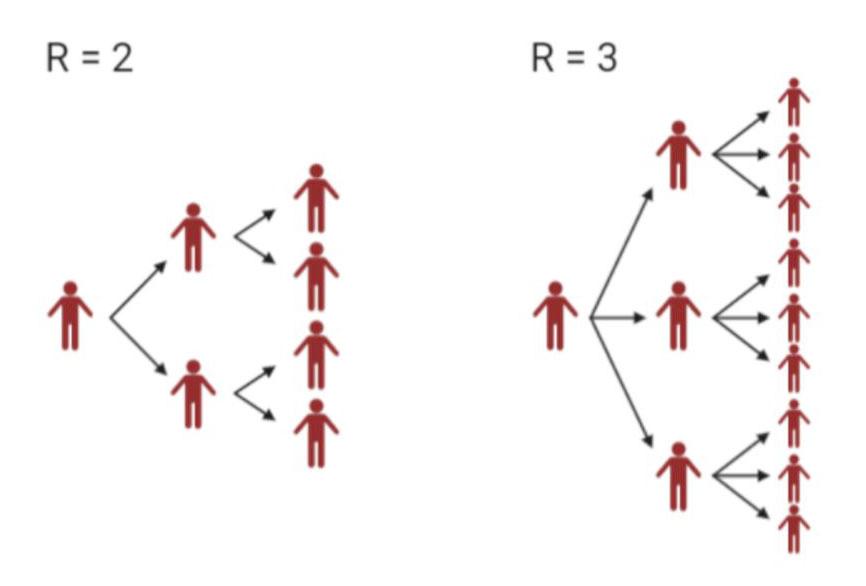
Vi skal no lage eit program som simulerer korleis smitteutviklinga kan gå føre seg. Realistiske modellar blir fort veldig kompliserte, så i programmet vårt bruker vi berre det såkalla R-talet for å finne smitta personar. R-talet seier oss kor mange personar ein sjuk person smittar vidare.
Under finn du eit program der du kan justere følgande verdiar:
R-talet ved starten av utbrotet
kor mange veker det tek før tiltak blir sette i verk
kva R-verdien blir etter at tiltaka er sette i verk
kor mange veker denne R-verdien varer
I starten vil R-talet ofte vere over 1, og etter at ein har sett i verk tiltak, bør det helst vere under 1. Prøv deg fram med ulike verdiar.
Kva må R-talet vere for at talet på smitta skal gå ned?
Obs! Bruk punktum (.) i staden for komma (,) viss du vel desimaltal som R-tal.
Tiltak som å stenge ned heile samfunnet kan ikkje halde fram i det uendelege. Før eller sidan må vi begynne å gå tilbake til kvardagen. I Noreg vart det letta på ein del tiltak før ein vaksine var ferdigutvikla. Det kan derfor vere interessant å utvide programmet til å ha fleire enn to fasar. Prøv å gjere det sjølv: Utvid programmet slik at det kan leggast inn fasar med varierande R-tal. Det kan vere lurt å bruke ei while-lykkje, slik at brukaren kan be om fleire periodar for kvar køyring.
Eksperimenter med R-tal mellom 1 og 4, og bruk til dømes eit intervall på 5 veker mellom kvar gong restriksjonane blir endra.
Programmet ditt er ikkje feil sjølv om det står "1e…" øvst i grafen. Sidan det er ein del smitta personar i befolkninga, og sidan veksten er eksponentiell, vil smittetalet fort eksplodere. Ved svært høge smittetal blir grafen markert øvst med "1e" og eit tal etterpå (t.d. 1e8, som betyr ). Talet viser altså kor mange nullar det skal vere etter verdiane på y-aksen.
Avgrensande faktorar

Heldigvis er det i verkelegheita ein del faktorar som vil avgrense smittespreiinga. Immunitet har vi allereie nemnt. I tillegg treng ikkje politikarane å vedta tiltak lang tid i førevegen. Ser dei at ting er i ferd med å kome ut av kontroll, kan dei setje i verk tiltak på kort varsel.
Modellen vår er relativt enkel, men gir forhåpentleg ei viss forståing av korleis smitte spreier seg. Skal vi få ein meir realistisk modell, må vi legge inn nokre fleire faktorar: Dei sjuke blir friske og kan ikkje smitte andre. Dei blir dessutan immune og kan ikkje bli sjuke ein gong til. Vaksinar blir utvikla og gitt til befolkninga. Dei vaksinerte kan ikkje bli sjuke og derfor heller ikkje smitte nokon.
Programmet under ser på utviklinga i den norske befolkninga og simulerer det samla talet nordmenn som har vore sjuke. Tre kurver blir genererte: éi for kvar av dei ovannemnde faktorane vi tek med i utrekningane.
Eit realistisk tal for talet på vaksinasjonar per veke er rundt 200 000. Då vil heile befolkninga i Noreg bli vaksinert i løpet av omtrent eit halvt år. Prøv å køyre simuleringa med ulike R-verdiar, og sjå kva som skjer.
Kvifor er det viktig at samfunnet klarer å halde R-talet lågt fram til alle er vaksinerte?
Kvifor flatar immunitetskurva ut før alle har blitt sjuke?
Korleis varierer immunitetskurva med R-talet?
Meir om flokkimmunitet hos Norsk Helseinformatikk
Relatert innhald
I dette spelet har du rolla som smittevernansvarleg i Kongsland. Det oppstår eit smitteutbrot, og spørsmålet blir: Kan du stoppe smitten?