Vinklar

Vinkel

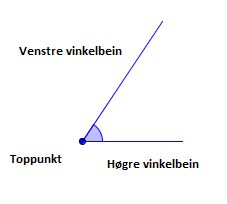
Når to strålar har felles endepunkt, dannar dei ein vinkel. Det felles endepunktet kallar vi vinkelens toppunkt. Strålane kallar vi vinkelbein.

Sett frå toppunktet får vi høgre vinkelbein og venstre vinkelbein.

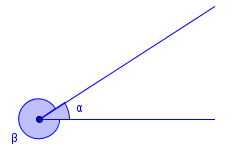
To strålar med felles endepunkt dannar eigentleg to vinklar. Sjå figuren til høgre. Når vi snakkar om vinkelen mellom to strålar, meiner vi vanlegvis den minste vinkelen, $\alpha$ på figuren.

Vinkelmål

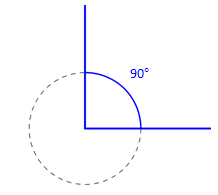
Det er vanleg å dele omkrinsen til ein sirkel i 360 deler, eller grader. Måling av vinklar byggjer på denne inndelinga.

Vi tenkjer oss at vi plasserer ein sirkel med sentrum i toppunktet til ein vinkel.

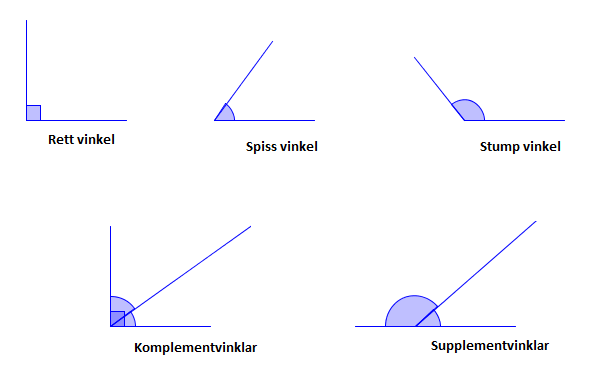
Ein vinkel som spenner over ein firedel av omkrinsen til sirkelen er då $\left(\frac{360}{4}\right)°=90°$. Denne vinkelen kallar vi ein rett vinkel.

Ein vinkel som spenner over halvparten av omkrinsen til sirkelen er 180°.

Ein vinkel mellom 0° og 90° kallar vi ein spiss vinkel.
Ein vinkel mellom 90° og 180° kallar vi ein stump vinkel.
To vinklar som til saman er 90° kallar vi komplementvinklar.
To vinklar som til saman er 180° kallar vi supplementvinklar.

Normalar

To linjer som danner ein vinkel på 90 grader med kvarandre, seier vi står normalt på kvarandre.

Vi skriv $a\perp b$.

Toppvinklar

Når to linjer skjer kvarandre, er to og to av dei fire vinklane som blir danna alltid like store.

På figuren er $v$ og $w$ supplementvinklar. Det tyder at

$\begin{array}{rcl}v+w& = & 180°\\ & & \\ v& =& 180°-w\end{array}$

Vi har også at

$\begin{array}{rcl}u+w& = & 180°\\ & & \\ u& =& 180°-w\end{array}$

Det må tyde at $u=v$ .

Same resonnement gir at $w=z$ .

Samsvarande vinklar

Ei linje $l$ skjer to andre linjer, $m$ og $n$. Av dei vinklane som blir danna, er to vinklar med ulike toppunkt samsvarande dersom overskjeringslinja utgjer anten høgre vinkelbein i begge vinklane eller venstre vinkelbein i begge vinklane.

På figuren er $\alpha$ (alfa) og $\beta$ (beta) eit par av samsvarande vinklar, og $\gamma$ (gamma) og $\delta$ (delta) er eit anna par av samsvarande vinklar. Overskjeringslinja $l$ er venstre vinkelbein i alle vinklane.

Samsvarande vinkler ved parallelle linjer

På figuren er $\alpha$ og $\beta$ samsvarande vinklar fordi venstre vinkelbein er felles
(linja $l$).

I tillegg er høgre vinkelbein, linjene $m$ og $n$ parallelle. Tenk deg at du roterer figuren 180° om midtpunktet mellom dei to skjeringspunkta.

Ser du at $\alpha =\beta$?

Når to parallelle linjer blir skorne av ei tredje linje, er dei samsvarande vinklane like store.
Og motsett, dersom samsvarande vinklar er like store, er de overskorne linjene parallelle.

Utfordring!

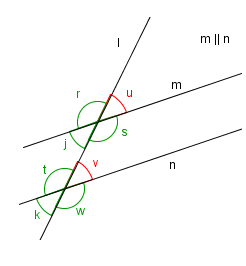
Kor store er vinklane $j, k, r, s, t$ og $w$ samanlikna med $u$ og $w$ når $m\left|\right|n$ ? Prøv å grunngi svara dine.

Når vinkelbein står parvis normalt på kvarandre

At summen av vinklane i ein trekant alltid er lik 180° (som vi viser seinare) kombinert med setning a som seier at toppvinklar er like store, gir følgjande nyttige setning: