Likningen for ei rett linje. Ettpunktsformelen
Fagstoff
Fagartikkel
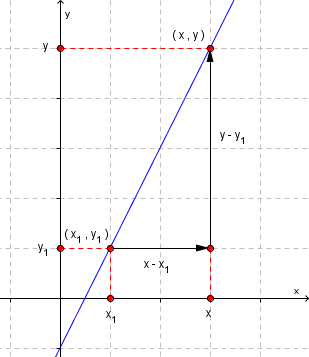
Likningen for ei rett linje gjennom to kjente punkt finner du ved å bruke formelen for stigningstallet sammen med ettpunktsformelen.
Åpne i fag:
Likningen for ei rett linje gjennom to kjente punkt finner du ved å bruke formelen for stigningstallet sammen med ettpunktsformelen.
