Arealformler
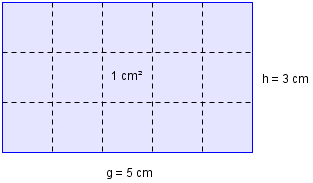
I et rektangel som er cm langt og cm høyt kan vi få plass til kvadrater som hver har et areal på cm². Det betyr at arealet er på cm².
Vi kan altså finne arealet til et rektangel ved å multiplisere grunnlinjen med høyden, eller det vi ofte kaller lengden med bredden.
Vi får en formel for arealet til et rektangel.
Husk at sidene må ha samme målenhet når vi skal regne ut arealet.
På figuren til høyre kan du sammenligne arealet til rektangelet med grunnlinje og høyde med arealet til trekanten med grunnlinje og høyde .
Du vil sannsynligvis bli overbevist om at arealet til rektangelet er dobbelt så stort som arealet til trekanten.
Siden arealet til rektangelet kan finnes ved å multiplisere grunnlinjen med høyden, , så er arealet til trekanten
Du kan nå ta for deg et parallellogram, en rombe og et trapes, og se om du kan lage arealformler for disse figurene på samme måte som for trekanter. Du kan sammenligne dine formler med formlene i skjemaet nedenfor.
Navn | Arealformel |
|---|---|
Kvadrat | |
Rektangel | |
Trekant | |
Parallellogram | |
Rombe | |
Trapes | |
Sirkel |
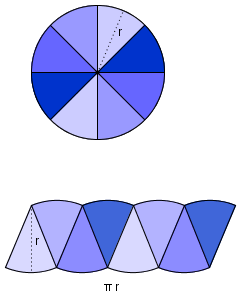
Det er ikke så lett å gjøre en sirkel om til et rektangel og på den måten finne formelen for arealet. Vi får likevel en brukbar tilnærming ved metoden vist i figuren.
Vi deler sirkelen inn i like sektorer. Så stiller vi sektorene annenhver opp og ned, slik at sektorene tilnærmet blir et parallellogram med grunnlinje tilnærmet lik
Jo flere sektorer vi inndeler sirkelen i, jo bedre blir tilnærmingen. Hvis vi deler sirkelen i veldig mange sektorer, får vi tilnærmet et rektangel.