Lineære funksjoner

Lineære funksjoner er funksjoner som beskriver rette linjer. Den generelle likningen for ei rett linje er y = ax + b.

Den generelle lineære funksjonen

En lineær funksjon er en funksjon der den uavhengige variabelen x bare finnes i første potens. Hvis vi tegner grafen til funksjonen, får vi ei rett linje.

Definisjon

En funksjon som kan skrives på formen

$f (x) = a x + b$

der koeffisientene $a, b \in ℝ$ , kalles en lineær funksjon eller en førstegradsfunksjon. Grafen til en førstegradsfunksjon blir ei rett linje.

Stigningstall og konstantledd

Før du leser videre, kan det være lurt å gjøre oppgave 1 på oppgavesiden om lineære funksjoner. Der kan du utforske hva endringer av koeffisientene a og b gjør med grafen til funksjonen.

Koordinatsystem med x-verdier fra minus 2 til 3 og y-verdier fra minus 4 til 1. Grafen til f av x er lik 2 x minus 2 er tegnet inn. Den er ei rett linje. Grafen skjærer andreaksen for y er lik minus 2 og x-aksen for x er lik 1. Stigningstallet a er lik 2 og punktet 0 og minus 2 er også tegnet inn. Illustrasjon.

På bildet har vi tegnet grafen til $f (x)$ for $a = 2$ og $b = - 2$ . Det betyr at $f (x) = 2 x - 2$ .

Legger du merke til at grafen skjærer y-aksen der $y = - 2$ ? Grafen skjærer andreaksen når $x = 0$ og
$y = f (0) = a \cdot 0 + b = b$ , det vil si i punktet $(0, b)$ .

Koeffisienten b kalles konstantleddet.

a viser hvor mye grafen stiger når x øker med 1 enhet.

Koeffisienten a kalles stigningstallet.

Hvis stigningstallet er negativt, synker grafen når x øker.

Mer om stigningstallet

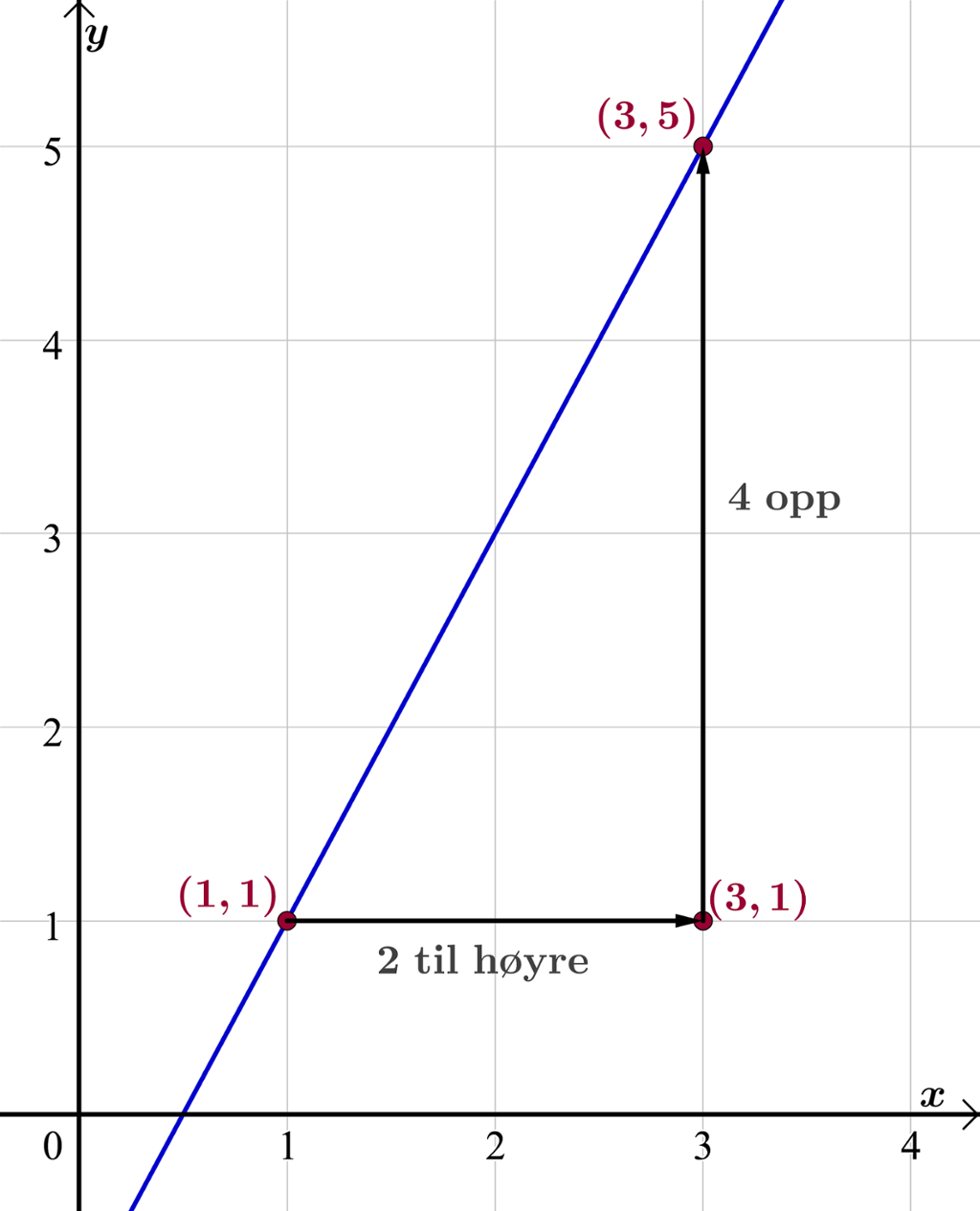
I et koordinatsystem der x-aksen går fra 0 til 4 og y-aksen går fra 0 til 5,5 er det tegnet ei rett linje. Linja går gjennom punktet med koordinatene 1 og 1 og punktet med koordinatene 3 og 5. Det er tegnet ei pil fra det første punktet med koordinatene 1 og 1 til punktet med koordinatene 3 og 1. Pila har tilhørende tekst 2 til høyre. Fra punktet med koordinatene 3 og 1 er det tegnet ei pil til punktet med koordinatene 3 og 5 på linja. Pila har tilhørende tekst 4 opp. Illustrasjon.

I avsnittet over ser vi at vi kan lese av stigningstallet ved å starte i et punkt på grafen, gå én enhet til høyre på x-aksen og så lese av hvor langt opp eller ned vi må gå for å treffe på grafen. Av og til kan det derimot være vanskelig å lese nøyaktig av ved å bare gå nøyaktig én enhet til høyre. Det kan derfor være nyttig å ha flere strategier for å finne stigningstallet. Vi ser på et nytt eksempel.

Ved å starte i for eksempel punktet (1, 1) og gå to enheter til høyre, må vi gå fire enheter oppover parallelt med y-aksen for igjen å treffe grafen. Stigningstallet blir

$a = \frac{4}{2} = 2$

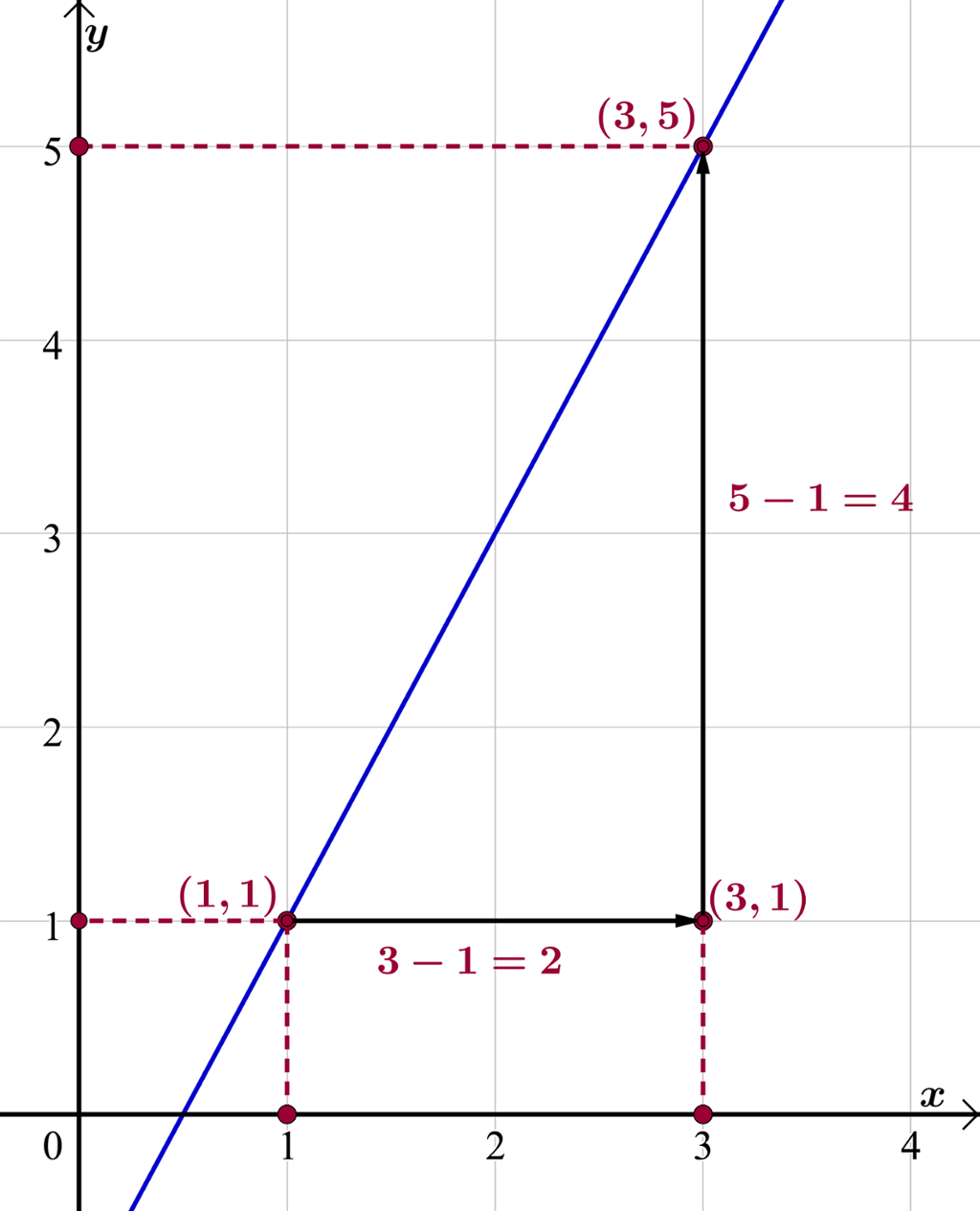
Dette kan vi også regne oss fram til med utgangspunkt i koordinatene til de to punktene på grafen

$a = \frac{5 - 1}{3 - 1} = \frac{4}{2} = 2$

I telleren har vi endring i y-verdi, og i nevneren har vi endring i x-verdi.

Endring i y-verdi dividert med endring i x-verdi gir alltid verdien for stigningstallet fordi stigningstallet er endring i y-retning per enhet på x-aksen.

Generell formel for stigningstallet

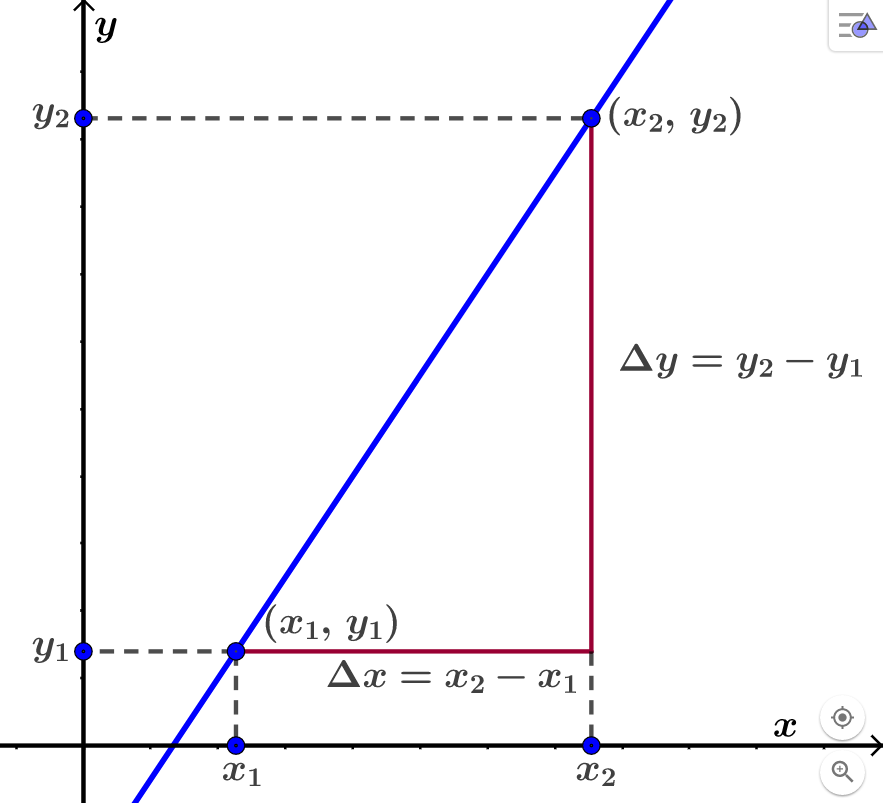
I et koordinatsystem uten tall på aksene er det tegnet ei rett linje. Linja går gjennom punktet med koordinatene x 1 og y 1 og punktet med koordinatene x 2 og y 2. Det er tegnet et vannrett linjestykke fra det første punktet med koordinatene x 1 og y 1 til punktet med koordinatene x 2 og y 1. Linjestykket har tilhørende tekst delta x er lik x 2 minus x 1. Fra punktet med koordinatene x 2 og y 1 er det tegnet et loddrett linjestykke til punktet med koordinatene x 2 og y 2 på den opprinnelige linja. Linjestykket har tilhørende tekst delta y er lik y 2 minus y 1. Illustrasjon.

Vi lar nå $(x_{1}, y_{1})$ og $(x_{2}, y_{2})$ være to vilkårlige punkter på linja. Legg merke til hvordan vi bruker indekser, 1 og 2, for å "navngi" punkt 1 og punkt 2.

Det er vanlig å la den greske bokstaven delta, $Δ$ , stå for endring.

Vi lar $Δ x = x_{2} - x_{1}$ være endring i x-verdi og $Δ y = y_{2} - y_{1}$ være endring i y-verdi.

Dette gir oss følgende formel:

Generell formel for stigningstallet til ei rett linje

$a = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} = \frac{Δ y}{Δ x}$

To spesialtilfeller

Du bør merke deg to spesialtilfeller av lineære funksjoner.

Det ene er når $b = 0$ . Da er $f (x) = a x$ , og y og x er proporsjonale størrelser. Tallet a kalles i dette tilfellet proporsjonalitetskonstanten.

Det andre spesialtilfellet er når $a = 0$ . Da er $f (x) = b$ , og grafen er parallell med x-aksen.

Å tegne grafen til en lineær funksjon

Vi skal se på hvordan vi kan tegne grafen til en lineær funksjon for hånd. Vi tar utgangspunkt i funksjonen $f (x) = - 2 x + 4$ og viser to ulike metoder.

Vi bruker verditabell

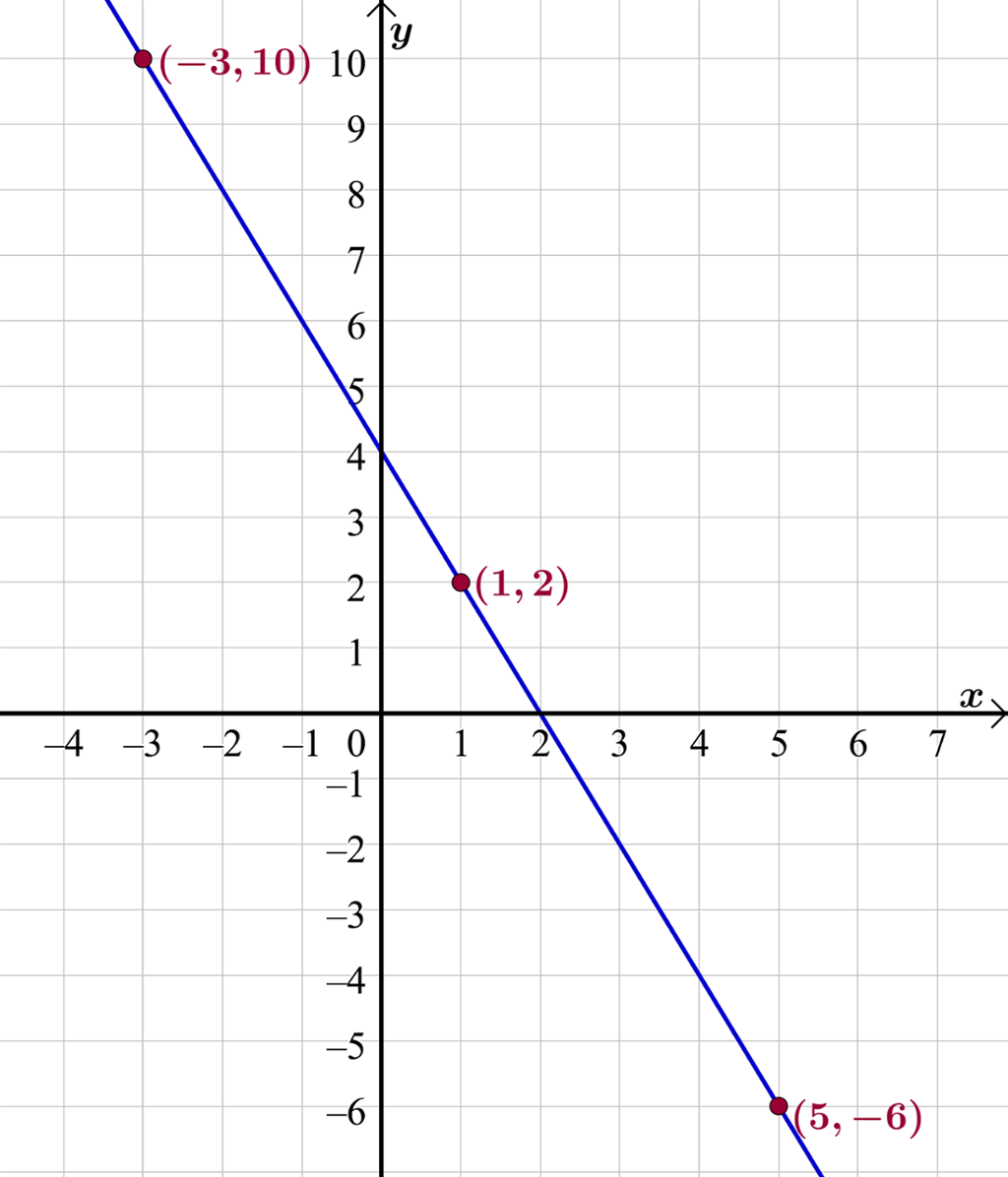
Grafen til en lineær funksjon gjennom punktet med koordinatene minus 3 og 10, punktet med koordinatene 1 og 2 og punktet med koordinatene 5 og minus 6 er tegnet i et koordinatsystem. Illustrasjon.

Vi vet at grafen blir ei rett linje. Da er det egentlig nok med to punkter i verditabellen siden ei rett linje er entydig bestemt av to punkter på linja. Det er likevel lurt å ta med et tredje punkt som kontroll. Dersom alle de tre punktene ligger på ei rett linje, vet vi at vi har regnet rett.

Vi fyller ut tabellen. Etterpå kan vi tegne inn punktene og trekke linja som går gjennom dem slik som på bildet:

Verditabell
x	f(x)
-3	10
1	2
5	-6

Vi bruker konstantledd og stigningstall

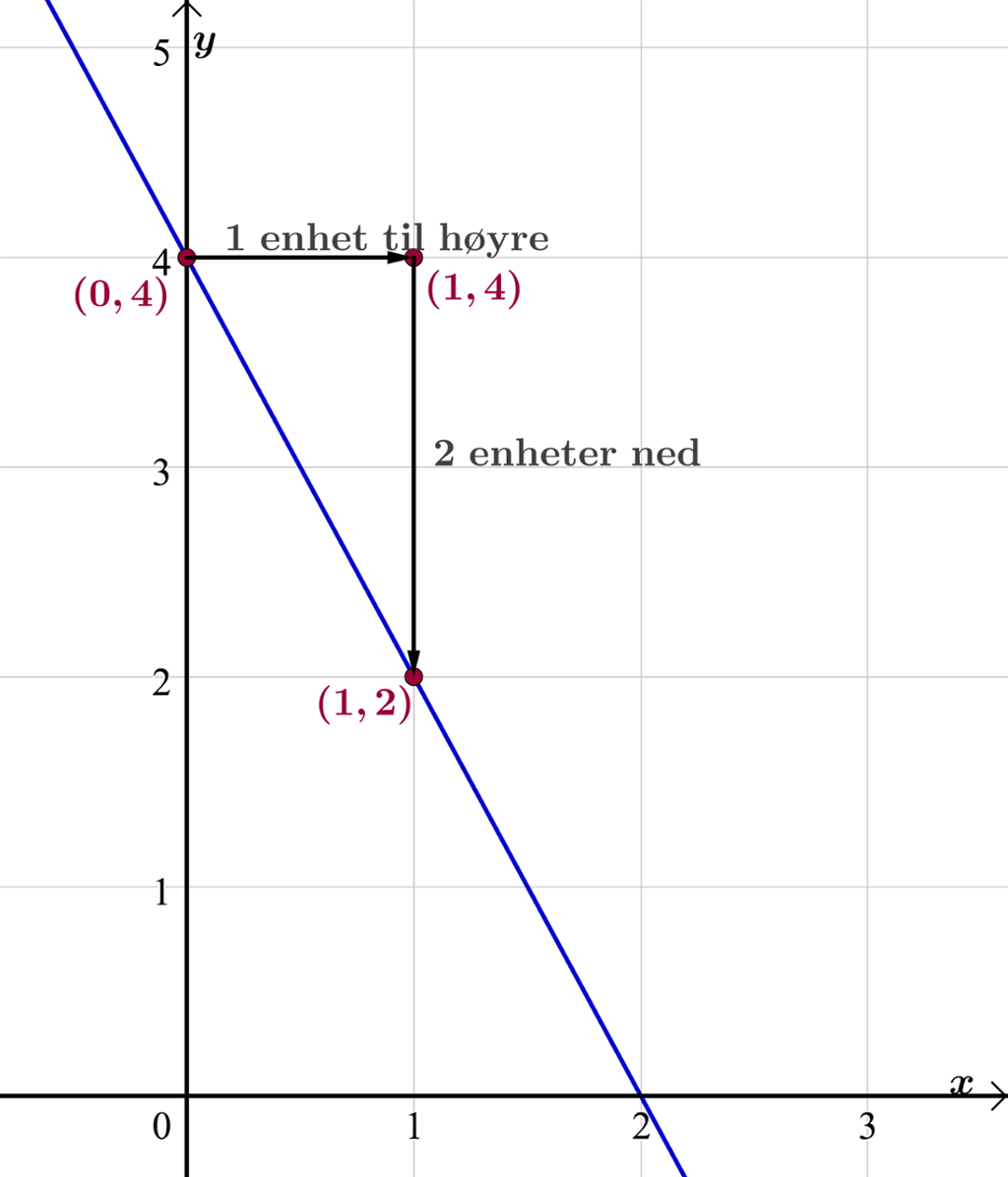
Grafen til en lineær funksjon som går gjennom punktene med koordinater 0 og 4 og 1 og 2 er tegnet i et koordinatsystem. Figuren viser at dersom man går 1 enhet til venstre fra punktet med koordinater 0 og 4, må man gå 2 enheter ned for å komme til grafen igjen. Illustrasjon.

Siden konstantleddet $b = 4$ , skjærer grafen andreaksen for $y = 4$ . Punktet (0, 4) ligger derfor på grafen.

Stigningstallet er $- 2$ . Vi tar utgangspunkt i punktet (0, 4), går en enhet til høyre, og stigningstallet forteller at vi må bevege oss parallelt med y-aksen 2 enheter ned for igjen å møte grafen. Vi kommer til punktet (1, 2). Vi har da to punkter på grafen og kan trekke linja gjennom disse punktene.

Oppsummering

En lineær funksjon er på formen $f (x) = a x + b$ .

a er stigningstallet og gir oss stigningen på linja.

b er konstantleddet og gir oss krysningspunktet med y-aksen.

Generell formel for stigningstallet er

$a = \frac{Δ y}{Δ x}$