Funksjoner representert ved grafer og verditabeller. Verdimengde

Vi ser på funksjonen $S$ gitt ved

$S\left(t\right)=160t D_s=\left[0, 100\right]$

Funksjonen er her representert med en formel.

Vi kan lage en verditabell ved først å velge ut noen verdier for $t$ som ligger i definisjonsområdet. Deretter kan vi regne ut de tilsvarende funksjonsverdiene, $S\left(t\right)$. Verditabellen nedenfor viser et utvalg av sammenhørende verdier for $t$ og $S\left(t\right)$.

Funksjonen er nå representert med en verditabell.

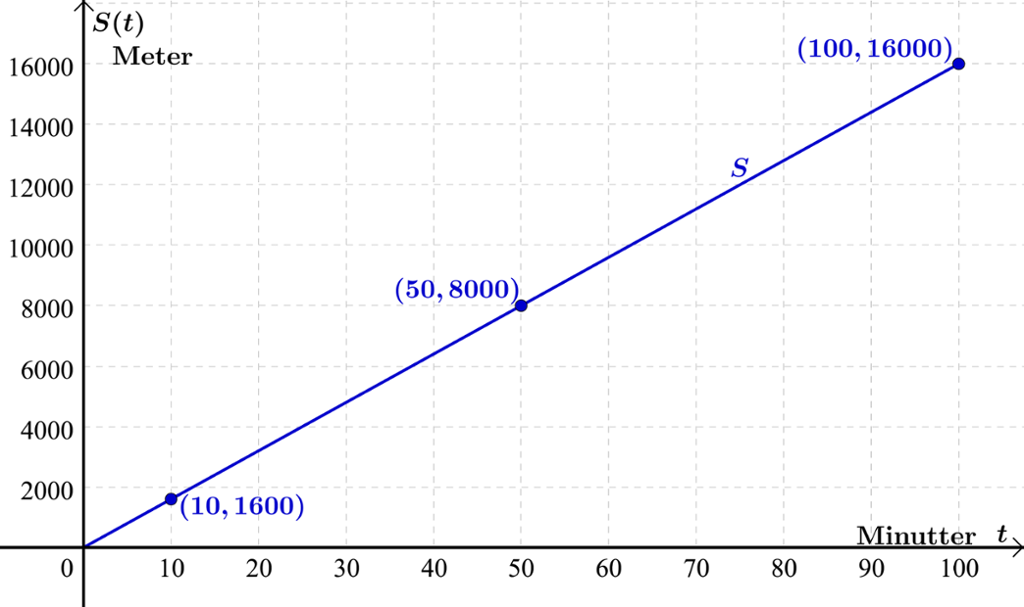
De sammenhørende verdiene fra verditabellen merker vi av som punkter i et koordinatsystem der $t$ avsettes langs førsteaksen og $S\left(t\right)$ langs andreaksen.

Aksene tilpasses slik at alle punktene i verditabellen «får plass» i grafvinduet.

I vårt eksempel ligger punktene på en rett linje. Vi trekker den rette linjen gjennom punktene. Denne linjen kalles for grafen til funksjonen.

Hvis punktene ikke ligger på en rett linje, tegner vi en kurve som går gjennom punktene.

Alle punktene som ligger på grafen til funksjonen viser sammenhørende verdier for $t$ og $S\left(t\right)$.

Funksjonen er nå representert med en graf.

Langs førsteaksen finner vi $t$-verdiene, altså definisjonsmengden til funksjonen. Langs andreaksen finner vi funksjonsverdiene $S\left(t\right)$. Vi ser at verdiene langs andreaksen går fra $0$ til $16000$ når $t$- verdiene gjennomløper definisjonsmengden, $D_s=\left[0, 100\right]$. Verdimengden er derfor $V_s=\left[0, 16 000\right]$.