Elektrisk effekt ved faseforskyvning

Vi tar opp tråden fra siden «Faseforskyvning i vekselspenningskretser», der vi har sett at

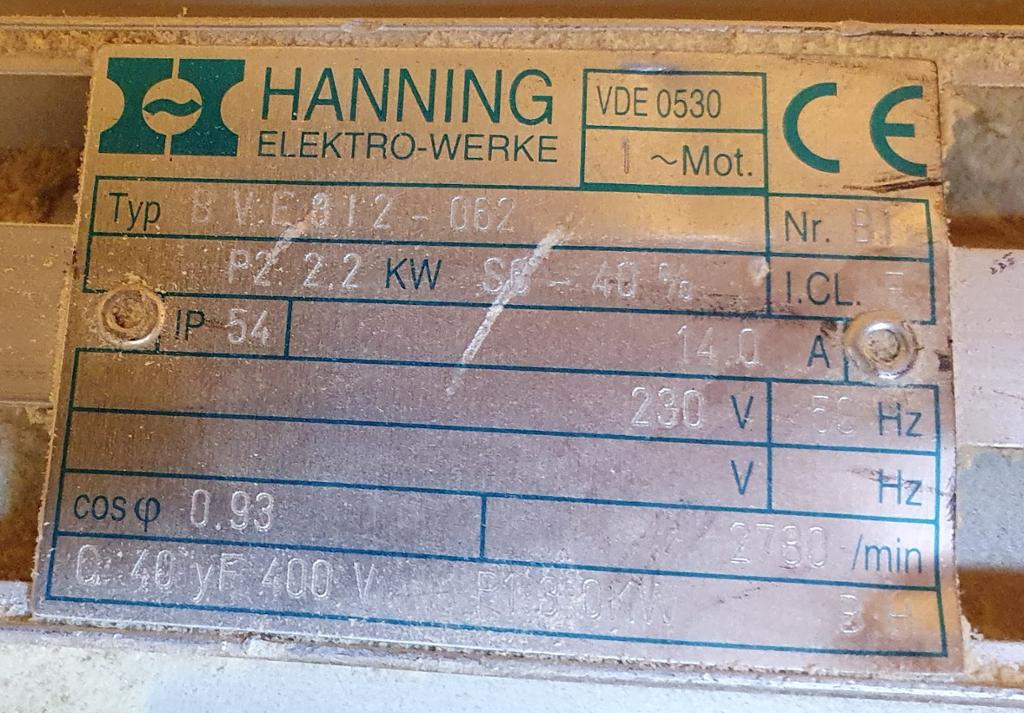
• strømmen I i en vekselspenningskrets med en elmotor ble målt til 3,4 A
• spenningen U over motoren ble målt til 230 V, den vanlige nettspenningen
• effekten P i motoren ble målt til 633 W med et wattmeter
• den elektriske effekten P er mindre enn produktet av spenning og strøm ($$$ P=U·I $$$ gjelder ikke her)
• spenningen U og strømmen I i en krets ikke har toppunkt samtidig når vi kobler til en elmotor; vi har faseforskyvning

Hva har faseforskyvningen å si for effekten? Husk at effekten er produktet av spenning og strøm til enhver tid, det vil si produktet av momentanverdiene av spenning og strøm. Men når strøm og spenning ikke når toppen samtidig, betyr det i målingene på motoren at når spenningen har toppverdien (vi bruker effektivverdiene som toppverdi) på 230 V, har ikke strømmen toppverdien på 3,4 A, og motsatt. Effekten blir derfor mindre enn produktet av disse to tallene.

Vi kan tegne strømmen og spenningen i et viserdiagram, eller et såkalt vektordiagram. Se nedenfor. Strømkurven og spenningskurven er tegnet i samme diagram, så høyden på kurvene spiller ikke noen rolle her. Dra i glidebryteren for faseforskyvning, og se hvordan strømsignalet flytter seg. Se samtidig hvordan den tilsvarende viseren for strøm i viserdiagrammet til venstre endrer seg. I tillegg kan du velge en t-verdi (et tidspunkt) med glidebryteren for målepunkt og flytte punktene på grafene for spenning og strøm. Samtidig kan du se hvordan de tilsvarende viserne ser ut i dette diagrammet. La faseforskyvningen være 0,002 s.

Den blå viseren viser spenningen, og den røde viseren viser strømmen. Viserne er tegnet i et sirkelformet diagram slik at spissen på viserne alltid har samme høyde som det tilsvarende punktet på grafene. Viseren for spenningen peker for eksempel rett opp når det tilhørende målepunktet er på toppunktet av spenningskurven. De peker rett ned når målepunktet er i et bunnpunkt. De peker rett til høyre når det tilhørende målepunktet er på et nullpunkt der spenningen eller strømmen er stigende.

Oppgave 1

Hvor lang tid tar det for spenningen å gjennomføre en hel svingning?

Oppgave 2

Hvor mange grader i viserdiagrammet tilsvarer en hel svingning?

Oppgave 3

Hvorfor blir det en vinkel mellom viserne for strøm og spenning?

Oppgave 4

Er viserne like lange i alle målepunktene? (Flytt målepunktene med glidebryteren til venstre, og observer.)

Oppgave 5

Hva er lengden av viseren for spenning og viseren for strøm?

Vi går tilbake til motoren som er koblet på nettspenningen. Vi ønsker å kunne finne effekten i motoren ved hjelp av de verdiene for spenning og strøm vi kan måle med et voltmeter og et amperemeter. Disse verdiene er etter det vi har funnet ut, lik lengden av viserne i viserdiagrammet. Problemet er bare at spenningen ikke er på topp samtidig som strømmen, og derfor blir den elektriske effekten mindre enn produktet av de to verdiene.

Oppgave 6

Bruk simuleringen over og sett t-verdien for målepunktet til 0,005 (der spenningskurven har et toppunkt). Faseforskyvningen skal fortsatt være 0,002 s eller 36 grader. Hvor finner vi den reelle strømmen $$$ I_r$$$ i sirkeldiagrammet?

Forklaring

Den reelle strømmen $$$ I_r$$$ er hosliggende katet i en rettvinklet trekant der strømviseren er hypotenusen, se figuren.

Oppgave 7

Hvordan regner vi ut strømmen $$$ I_r$$$ ut fra lengden I på strømviseren og fasevinkelen, som vi kaller $$$ \phi $$$?

Oppgave 8

Hva blir effekten i motoren når vi måler strømmen til 3,4 A og spenningen er 230 V?

Vi har altså at på grunn av faseforskyvningen av strømmen blir effekten P i motoren

$$$ P=U·I·\cos \phi $$$

Hvordan finner vi denne faseforskyvningen? Ofte er verdien for $$$ \cos \phi $$$ oppgitt på typeskiltet til elektromotoren, slik som eksempelet under viser.

$$$ \cos \phi $$$ kalles ofte effektfaktoren fordi det er den faktoren vi må multiplisere måleverdiene for strøm og spenning med for å få det vi kaller den aktive effekten, den effekten vi kan ta ut i motoren. Den aktive effekten måles i W (watt), som er den vanlige enheten for effekt.

Dersom vi multipliserer måleverdiene for strøm og spenning uten å ta med effektfaktoren, får vi det vi kaller tilsynelatende effekt eller tilført effekt, som har symbolet S. Dette er en størrelse som ikke har betydning i strømkretsen, og for å skille den fra den aktive effekten P bruker vi enheten VA (voltampere) i stedet for watt.

$$$ S=U·I$$$

Vi kan si at det er denne effekten som skulle ha blitt utviklet i kretsen med de verdiene vi har for strøm og spenning.

Oppgave 9

Hvor stor er effektfaktoren i eksempelet vårt?

Oppgave 10

Finn en formel for effektfaktoren $$$ \cos \phi $$$ uttrykt ved den aktive effekten P og den tilsynelatende effekten S.

Oppgave 11

Forklar hvordan du kan tegne en rettvinklet trekant der faseforskyvningen $$$ \phi $$$ er en av vinklene, og P og S er to av de tre sidene i trekanten.

På figuren har vi tegnet trekanten i oppgaven over.

Hva så med den motstående kateten i trekanten? Dette representerer det vi kaller reaktiv effekt som kommer i stand på grunn av selvinduksjonen i kretsen. Den reaktive effekten, som ofte har symbolet Q, kan vi ikke utnytte. For å skille reaktiv effekt fra de to andre måles denne i «voltampere reaktiv effekt», var.

Aktiv effekt P: Den effekten vi kan utnytte. Formel: $$$ P=U·I·\cos \phi $$$. Måles i W.

Reaktiv effekt Q: Motstående katet i effekttrekanten. Måles i var.

Tilsynelatende/tilført effekt S: Produktet av spenning U og strøm I i kretsen. Formel: $$$ S=U·I$$$. Måles i VA.

Effektfaktor: $$$ \cos \phi $$$ der $$$ \phi $$$ er faseforskyvningen på strømmen i forhold til spenningen målt i grader.