Fagartikkel
Sammenhengen mellom andregradslikninger og andregradsfunksjoner
Nullpunktene til en funksjon finner vi der grafen skjærer x-aksen der funksjonsuttrykket er null.
Bilde: Olav Kristensen, Stein Aanensen / CC BY-NC-SA 4.0
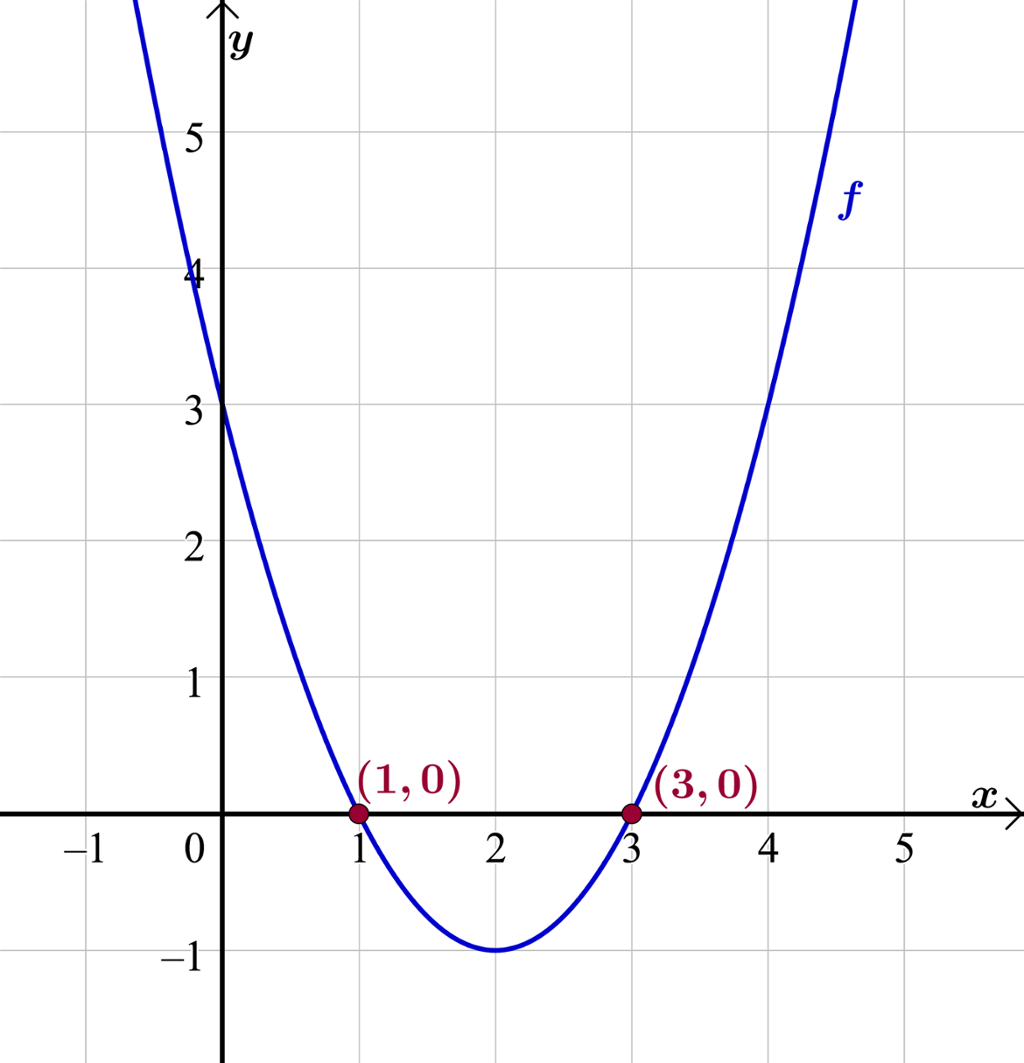
Vi ser på grafen til funksjonen .
Grafen skjærer førsteaksen når og når . Dette er nullpunktene til .
I GeoGebra kan du finne nullpunktene grafisk med kommandoen "Nullpunkt[f]".
Ved regning finner vi nullpunktene ved å løse likningen
.
Det betyr at vi må løse andregradslikningen
Vi bruker abc-formelen og får
Det betyr at funksjonen har nullpunktene og .
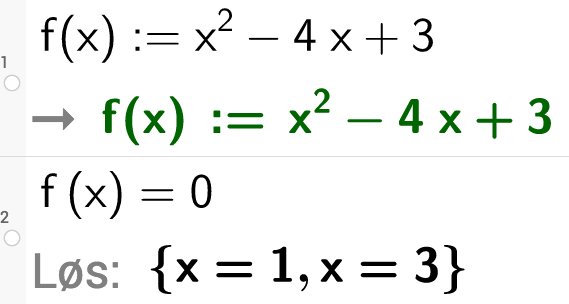
Bilde: Olav Kristensen, Stein Aanensen / CC BY-NC-SA 4.0
I GeoGebra kan vi finne nullpunktene ved regning ved først å definere funksjonen i CAS-vinduet. Husk da å skrive «kolon-lik».
Merk: Du trenger ikke definere funksjonen hvis du allerede har den i algebrafeltet.
Deretter bruker du kommandoen «Løs» på likningen .