Regresjon
Regresjonsanalyse eller regresjon betyr for oss at vi har noen samhørende verdier for to variabler og prøver å finne en sammenheng mellom dem, en sammenheng i form av en funksjon. Dette er det motsatte av progresjon, som vi vanligvis gjør der vi har modellen (funksjonen), og regner ut samhørende verdier for de to variablene.
I eksempelet nedenfor kaster Camilla en ball opp i lufta. Vi måler høyden ballen har
Camilla kaster en ball rett opp i lufta. Tabellen viser ballens høyde
| 0 | 1,8 |
| 0,5 | 7,6 |
| 1 | 11 |
| 1,5 | 11,9 |
| 2 | 10,4 |
| 2,5 | 6,4 |
| 3 | 0 |
Her har vi samhørende verdier for de to variablene tid
Regresjon med GeoGebra
Vi skriver tallene inn i regnearkdelen i GeoGebra, markerer tallene og velger verktøyet "Regresjonsanalyse" fra den andre verktøymenyen øverst. Se figuren nedenfor.
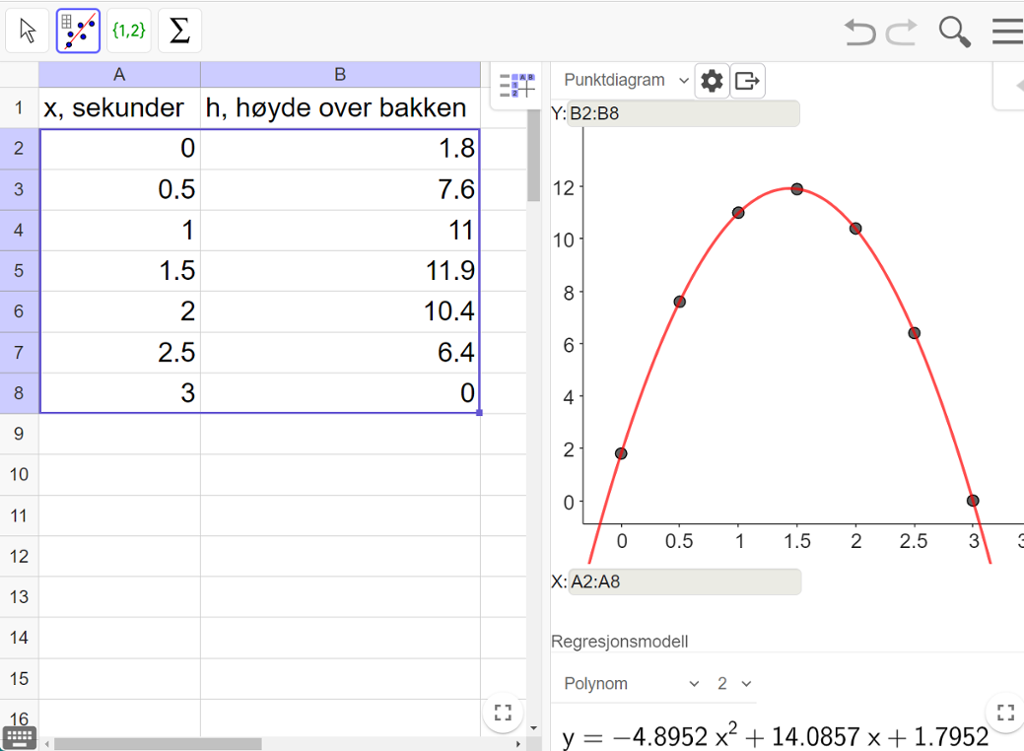
Først vises bare punktene fra regnearket. Grafen får vi først når vi velger en regresjonsmodell. Siden punktene ser ut som de kan ligge på en parabel, velger vi "Polynom" og "2" for å få en andregradsfunksjon. GeoGebra beregner da at den andregradsfunksjonen som passer best med tallene, er
Vi kan se at grafen til denne funksjonen passer svært godt til målepunktene. Det skjer ikke alltid.
For å få grafen over i det vanlige grafikkfeltet trykker vi på knappen med en firkant og ei pil på øverst i regresjonsanalyseverktøyet og velger "Kopier til grafikkfeltet". Da kan vi lage en skikkelig grafisk framstilling av resultatene og sette navn på aksene.
Regresjon med Python
Regresjon med Python kan gjøres på flere måter. Her har vi valgt å bruke metoden curve_fit fra scipy.optimize selv om den gir oss mer data enn vi skal bruke her.
Metoden er basert på at vi angir i koden hva slags type funksjon som skal brukes i den matematiske modellen. Dette gjøres ved å definere modellen som en egendefinert pythonfunksjon, som vi velger å kalle modell. I vårt tilfelle ønsker vi å tilpasse målingene til en andregradsfunksjon av typen modell kan da se slik ut:
1def modell(x,a,b,c): 2 return a*x**2 + b*x + c
Parametrene til modell er først den frie variabelen x, deretter konstantene som skal brukes i modellfunksjonen, som vi naturlig nok kaller a, b og c. Funksjonen modell brukes av metoden curve_fit sammen med ei liste med curve_fit gir tilbake to lister. Den ene inneholder de tre konstantene a, b og c som gjør at den matematiske funksjonen vi definerte i modell, passer mest mulig med måledataene. Den andre lista inneholder de såkalte kovariansene, som vi ikke skal bruke her.
Koden for hele programmet kan se slik ut:
1 # importerer nødvendige bibliotek 2from scipy.optimize import curve_fit 3import numpy as np 4import matplotlib.pyplot as plt 5 6 # lager funksjonen som beskriver modellen 7def modell(x,a,b,c): 8 return a*x**2 + b*x + c 9 10 # legger inn måledataene i lister 11x_verdier = [0,0.5,1,1.5,2,2.5,3] 12y_verdier = [1.8,7.6,11,11.9,10.4,6.4,0] 13 14 # bruker metoden curve_fit og legger resultatene i to lister 15konstanter,kovarians = curve_fit(modell,x_verdier,y_verdier) 16 17 # henter ut konstantene fra lista konstanter 18a, b, c = konstanter 19 20 # lager utskrift av funksjonen 21print(f"Funksjonen blir h(x) = {a:.2f}x^2 {b:+.2f}x {c:+.2f}.") 22 23 # plotter data 24plt.plot(x_verdier,y_verdier,'o', label = "Målinger") 25 26 # plotter modell 27x_array = np.linspace(min(x_verdier),max(x_verdier),300) 28y_array = modell(x_array,a,b,c) 29plt.plot(x_array,y_array,"brown", label = "Modell") 30plt.legend(bbox_to_anchor=(1,1)) 31plt.xlabel("$x$, tid i sekunder") # tittel på x-aksen 32plt.ylabel("$h$, høyde i meter ") 33plt.grid(True) 34plt.show()
Kjøring av koden gir følgende utskrift:
"Funksjonen blir h(x) = -4.90x^2 +14.09x +1.80."
Vi får samme funksjon