Fagstoff

Krumningsforhold og vendepunkter. Dobbeltderiverttesten

Vi kan ha god nytte av den andrederiverte, eller den dobbeltderiverte, til en funksjon.

Funksjonen $f$ er gitt ved

$f (x) = \frac{1}{3} x^{3} - \frac{1}{2} x^{2} - 2 x + 1$

Denne funksjonen er også drøftet i eksempel 2 på sida Analyse av polynomfunksjoner ved regning.

Vi deriverer funksjonen to ganger. Da får vi den andrederiverte eller den dobbeltderiverte $f^{''} (x)$ . Legg merke til skrivemåten, nå med to apostrofer.

$\begin{array}{l} f (x) = \frac{1}{3} x^{3} - \frac{1}{2} x^{2} - 2 x + 1 \\ f^{'} (x) = x^{2} - x - 2 \\ f^{''} (x) = 2 x - 1 \end{array}$

Vi tegner fortegnslinja til $f^{''} (x)$ og grafen til selve funksjonen i det samme koordinatsystemet.

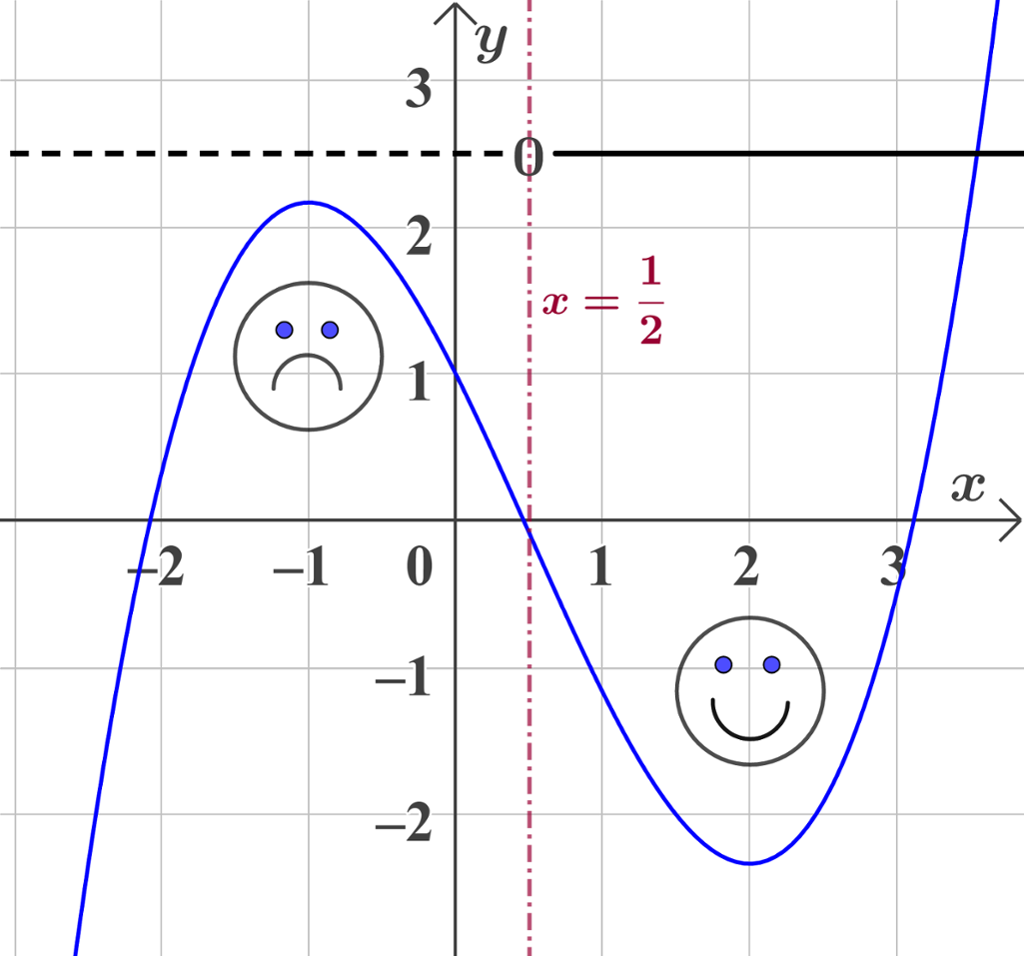
Grafen til f av x er lik 1 tredels x i tredje minus 1 halv x i andre minus 2 x pluss 1 er tegnet i et koordinatsystem for x-verdier mellom minus 2,5 og 3,5. Fortegnslinja for f dobbeltderivert av x er også tegnet. Linja er stiplet når x er mindre enn en halv, null når x er lik 1 halv og heltrukken når x er større enn en halv. Et surt fjes er tegnet i det området der grafen til f vender sin hule side ned, og et smilefjes er tegnet i det området der grafen til f vender sin hule side opp. Linja x er lik 1 halv er tegnet inn. Skjermutklipp.

Det viser seg at

en graf vender den hule sida si opp når $f^{''} (x) > 0$ . Den krummer oppover.
en graf vender den hule sida si ned når $f^{''} (x) < 0$ . Den krummer nedover.
en graf kan ha et vendepunkt når $f^{''} (x) = 0$

At grafen vender den hule sida si opp, $f^{''} (x) > 0$ , betyr at den deriverte vokser. Det vil si at selve funksjonen enten vokser mer og mer eller avtar mindre og mindre.

At grafen vender den hule sida si ned, $f^{''} (x) < 0$ , betyr at den deriverte avtar. Det vil si at selve funksjonen avtar mer og mer eller vokser mindre og mindre.

Vendepunkt

Et punkt på grafen der grafen skifter mellom å vende den hule sida si ned og å vende den hule sida si opp, eller motsatt, kalles et vendepunkt. Vi kan også si at grafen endrer krumning.

Den deriverte (dersom den eksisterer!) har enten sin største verdi eller sin minste verdi i vendepunktet. Det vil si at funksjonen vokser raskest eller avtar raskest i vendepunktet.

Har vi alltid et vendepunkt dersom den dobbelderiverte er lik 0?

Svar

Nei, det har vi ikke.

Tegn grafen til $f (x) = x^{4}$ i GeoGebra. Du vil se at grafen "er blid" overalt.

Men hvis vi dobbeltderiverer, får vi

$\begin{array}{rcl} f (x) & = & x^{4} \\ f^{'} (x) & = & 4 x^{3} \\ f^{''} (x) & = & 12 x^{2} \end{array}$

Det vil si at den dobbeltderiverte har et nullpunkt for $x = 0$ uten at funksjonen har et vendepunkt.

Det vi må se på her, er om den dobbelderiverte skifter fortegn i nullpunktet, siden et vendepunkt er definert som et punkt på grafen der grafen endrer krumning. $12 x^{2} \geq 0$ for alle $x \in ℝ$ , så derfor har vi ikke et vendepunkt i dette tilfellet.

Kan vi ha et vendepunkt uten at den dobbeltderiverte er lik 0?

Svar

Ja, det kan vi ha.

Tegn grafen til $g (x) = \sqrt[5]{x^{3}}$ i GeoGebra. Ser du at grafen har den hule sida opp for $x < 0$ og den hule sida ned for $x > 0$ ?

Hvis vi deriverer to ganger, vil vi se at hverken den deriverte eller den dobbeltderiverte er definert i punktet $x = 0$ .

Men selve funksjonen er definert og har et vendepunkt for $x = 0$ .

Vi husker at vi har et vendepunkt dersom funksjonen endrer krumning i dette punktet, altså dersom den dobbeltderiverte har ulikt fortegn på hver side av punktet. Det kan skje i et punkt der den dobbeltderiverte er null, eller i et punkt der den dobbeltderiverte ikke er definert, slik som i dette tilfellet.

Under har vi tegnet grafen til $g (x)$ sammen med grafen til den dobbeltderiverte:

På bildet er g av x lik femterota av x i tredje tegnet inn som grønn graf. Den dobbeltderiverte av x er tegnet inn som blå graf. Skjermutklipp.

Definisjon av vendepunkt

Vi ønsker oss en formell definisjon på hva som er et vendepunkt. Vi har til nå vist at vi må ha et punkt på grafen der den dobbelderiverte skifter fortegn. Legg merke til at det ikke er et krav at den deriverte eller den dobbelderiverte må eksistere i dette punktet, men det er et krav at selve funksjonen må være definert her. I tillegg til dette er det et krav om at funksjonen må være kontinuerlig i dette punktet. Noen matematikere krever i tillegg at det skal være mulig å tegne en tangent i et punkt for at det skal kunne defineres som et vendepunkt, men vi velger her definisjonen som kun krever kontinuitet.

Da kan vi få følgende definisjon:

Et punkt $(a, f (a))$ på grafen til en funksjon $f (x)$ er et vendepunkt dersom $f (x)$ er kontinuerlig for $x = a$ og $f^{''} (x)$ har motsatt fortegn for $x < a og x > a$ i et område rundt $a$ .

Vendetangent

I oppgaver blir vi ofte bedt om å finne likningen for en vendetangent. En vendetangent er tangenten til funksjonen i et vendepunkt.

Eksempel

Vi vil finne likningen for vendetangenten til funksjonen $f$ gitt ved

$f (x) = \frac{1}{3} x^{3} - \frac{1}{2} x^{2} - 2 x + 1$

Dette er samme funksjonen som vi brukte i eksempelet øverst på sida. Vi deriverer først funksjonen to ganger.

$\begin{array}{rcl} f (x) & = & \frac{1}{3} x^{3} - \frac{1}{2} x^{2} - 2 x + 1 \\ f^{'} (x) & = & x^{2} - x - 2 \\ f^{''} (x) & = & 2 x - 1 \end{array}$

Vi setter så den dobbeltderiverte lik null.

$\begin{array}{rcl} f^{''} (x) & = & 0 \\ 2 x - 1 & = & 0 \\ x & = & \frac{1}{2} \end{array}$

Vi har også at $f^{''} (0) = - 1$ og $f^{''} (1) = 2 \cdot 1 - 1 = 1$ . Det viser at vi har et vendepunkt for $x = \frac{1}{2}$ .

$f (\frac{1}{2}) = \frac{1}{3} {(\frac{1}{2})}^{3} - \frac{1}{2} {(\frac{1}{2})}^{2} - 2 (\frac{1}{2}) + 1 = - \frac{1}{12}$

Det betyr at koordinatene til vendepunktet er $(\frac{1}{2}, - \frac{1}{12})$ .

Vi regner så ut stigningstallet til tangenten i vendepunktet:

$f^{'} (\frac{1}{2}) = {(\frac{1}{2})}^{2} - \frac{1}{2} - 2 = - \frac{9}{4}$

Nå vet vi at vendetangenten går gjennom punktet $(\frac{1}{2}, - \frac{1}{12})$ og har stigningstallet $- \frac{9}{4}$ . Vi kan da bruke ettpunktsformelen og finne likningen for tangenten.

$\begin{array}{rcl} y - y_{1} & = & a (x - x_{1}) \\ y - (- \frac{1}{12}) & = & - \frac{9}{4} (x - \frac{1}{2}) \\ y + \frac{1}{12} & = & - \frac{9}{4} x + \frac{9}{8} \\ y & = & - \frac{9}{4} x + \frac{9}{8} - \frac{1}{12} \\ y & = & - \frac{9}{4} x + \frac{25}{24} \end{array}$

Vi har til slutt tatt med en oversikt over fortegnslinja til selve funksjonsuttrykket sammen med fortegnslinjene til den første- og andrederiverte. Disse er tegnet inn i koordinatsystemet sammen med $f (x)$ .

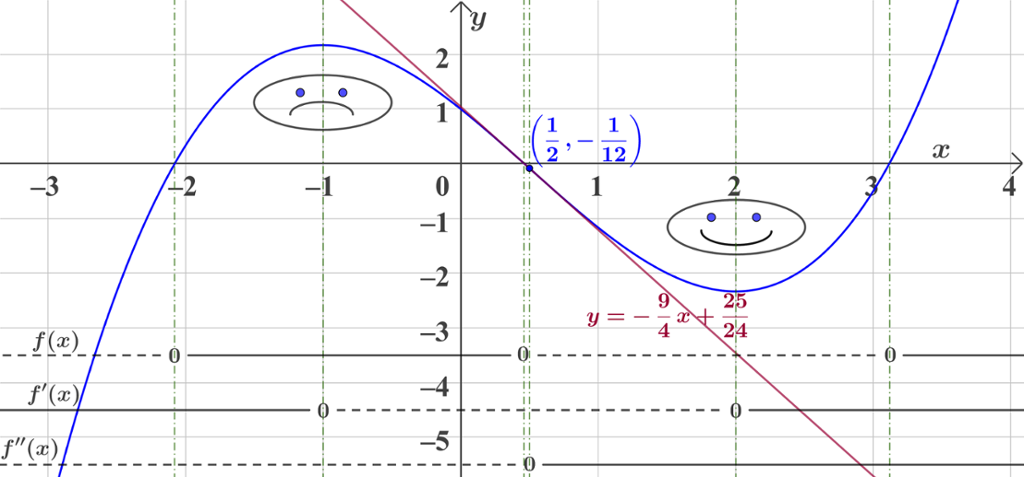
Grafen til f av x er lik 1 tredels x i tredje minus 1 halv x i andre minus 2 x pluss 1 er tegnet i et koordinatsystem for x-verdier mellom minus 3 og 3,5. Fortegnslinja for f dobbeltderivert av x er også tegnet. Linja er stiplet når x er mindre enn en halv, null når x er lik 1 halv og heltrukken når x er større enn en halv. Fortegnslinja for f derivert av x er tegnet. Linja er heltrukken når x er mindre enn minus 1, null når x er lik minus 1, stiplet når x er større enn minus 1 og mindre enn 2, null når x er lik 2 og heltrukken når x er større enn 2. Fortegnslinja til f av x er også tegnet . Den er stiplet når x er mindre enn minus 2,1, null når x er lik 2,1, heltrukken når x er større enn minus 2,1 og mindre enn 0,45, null når x er lik 0,45, stiplet når x er større enn 0,45 og mindre enn 3,15, null når x er lik 3,15 og heltrukken når x er større enn 3,15. Et surt fjes er tegnet i det området der grafen til f vender sin hule side ned, og et smilefjes er tegnet i det området grafen til f vender sin hule side opp. Skjermutklipp.

På grunnlag av fortegnslinjene er det mulig å tegne en skisse av grafen. Motsatt kan vi ut fra grafen tegne de tre fortegnslinjene. Ved hjelp av grafen kan vi altså tolke grunnleggende egenskaper ved funksjonen.

Toppunkt eller bunnpunkt? Dobbeltderiverttesten

CAS-utregning med GeoGebra. På linje 1 er det skrevet f av x kolon er lik 1 tredels x i tredje minus 1 halv x i andre minus 2 x pluss 1. Svaret er det samme. På linje 2 er det skrevet f derivert av x er lik 0. Svaret med N Løs er x er lik minus 1 eller x er lik 2. På linje 3 er det skrevet f dobbeltderivert av minus 1. Svaret er minus 3. På linje 4 er det skrevet f dobbeltderivert av 2. Svaret er 3. På linje 5 er det skrevet f av minus 1. Svaret er 13 seksdeler. På linje 6 er det skrevet f av 2. Svaret er minus 7 tredeler. Skjermutklipp.

Vi har brukt fortegnslinje til den deriverte for å avgjøre om et ekstremalpunkt er et toppunkt eller et bunnpunkt.

Den dobbeltderiverte gir oss en ny metode for å avgjøre dette.

Funksjonen $f (x)$ er definert i CAS-vinduet.

Siden $f^{'} (- 1) = 0$ og $f^{''} (- 1)$ er negativ, har grafen hul side ned og et toppunkt for $x = - 1$ .

Siden $f^{'} (2) = 0$ og $f^{''} (2)$ er positiv, har grafen hul side opp og et bunnpunkt for $x = 2$ .

Grafen har toppunkt $(- 1, \frac{13}{6}) .$

Grafen har bunnpunkt $(2, - \frac{7}{3}) .$

CC BY-SASkrevet av Olav Kristensen, Stein Aanensen og Tove Annette Holter.

Sist faglig oppdatert 16.08.2023