Grafisk løsning av likningssett
3.2.60
Løs likningssettene grafisk.
a)
vis fasit
Vi ordner hver likning og skriver som en funksjon av :
Så tegner vi grafene og finner skjæringspunktet:
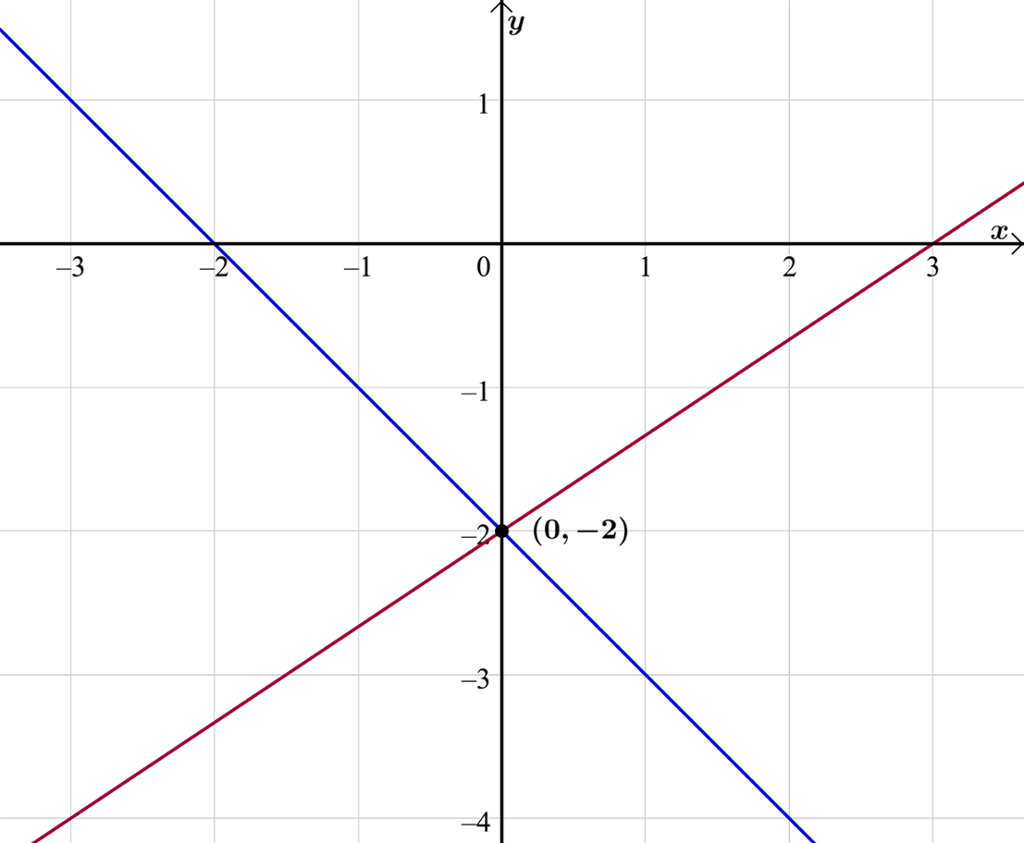
Løsning på likningssettet er
b)
vis fasit
Vi ordner hver likning og skriver som en funksjon av :
Så tegner vi grafene og finner skjæringspunktet:
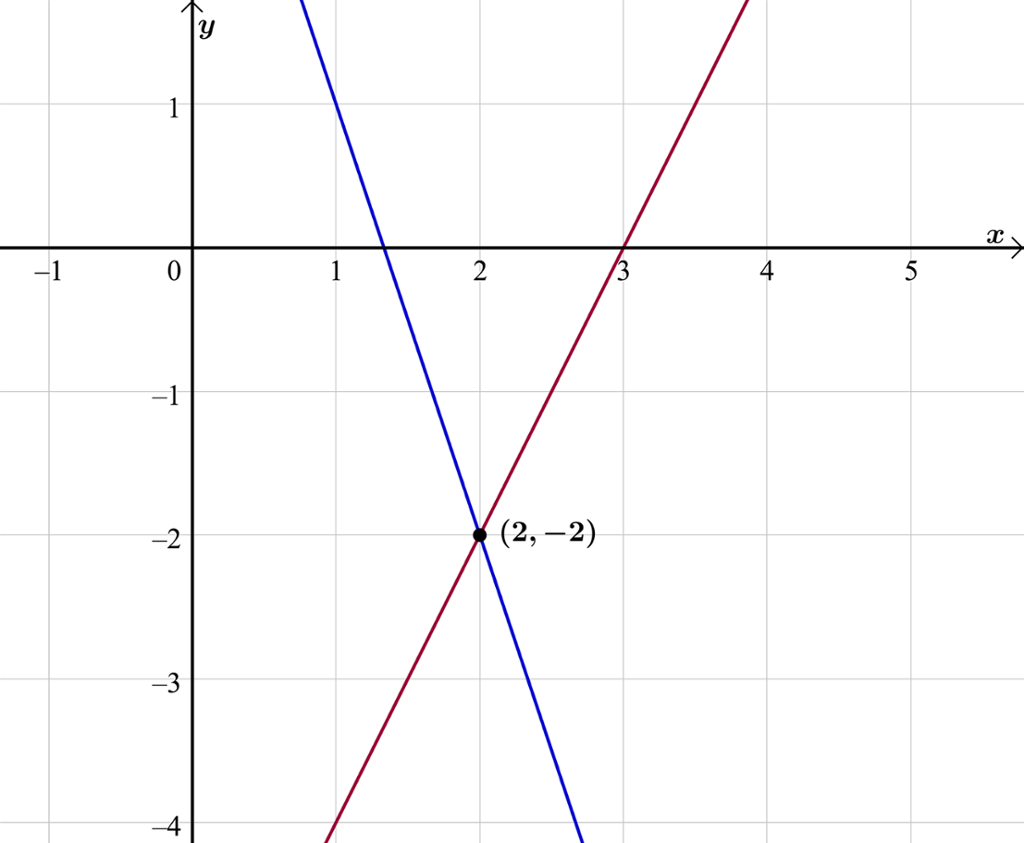
Løsning på likningssettet er .
c)
vis fasit
Vi ordner hver likning og skriver som en funksjon av :
Så tegner vi grafene og finner skjæringspunktet:
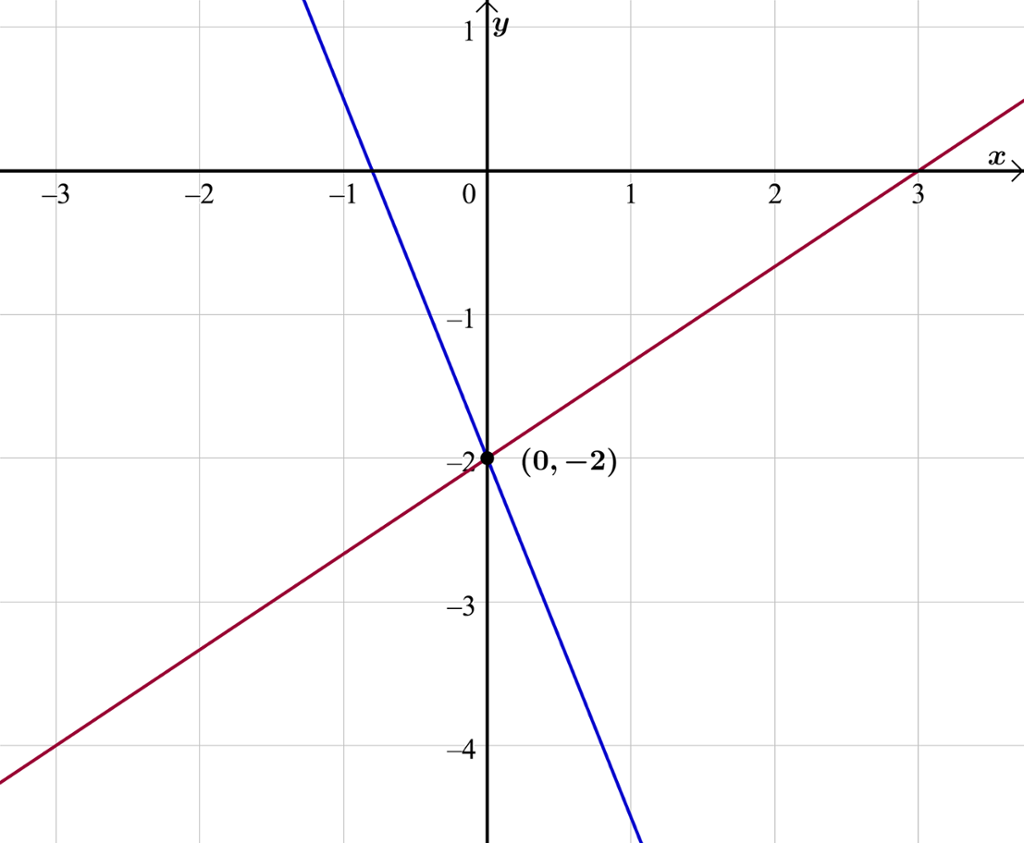
Løsning på likningssettet er
d)
vis fasit
Vi ordner hver likning og skriver som en funksjon av :
Grafene får samme funksjonsuttrykk. Det vil si at de faller sammen Alle punkt som ligger på linja er løsninger av likningssettet.
e)
vis fasit
Vi ordner hver likning og skriver som en funksjon av :
Så tegner vi grafene og finner skjæringspunktet:
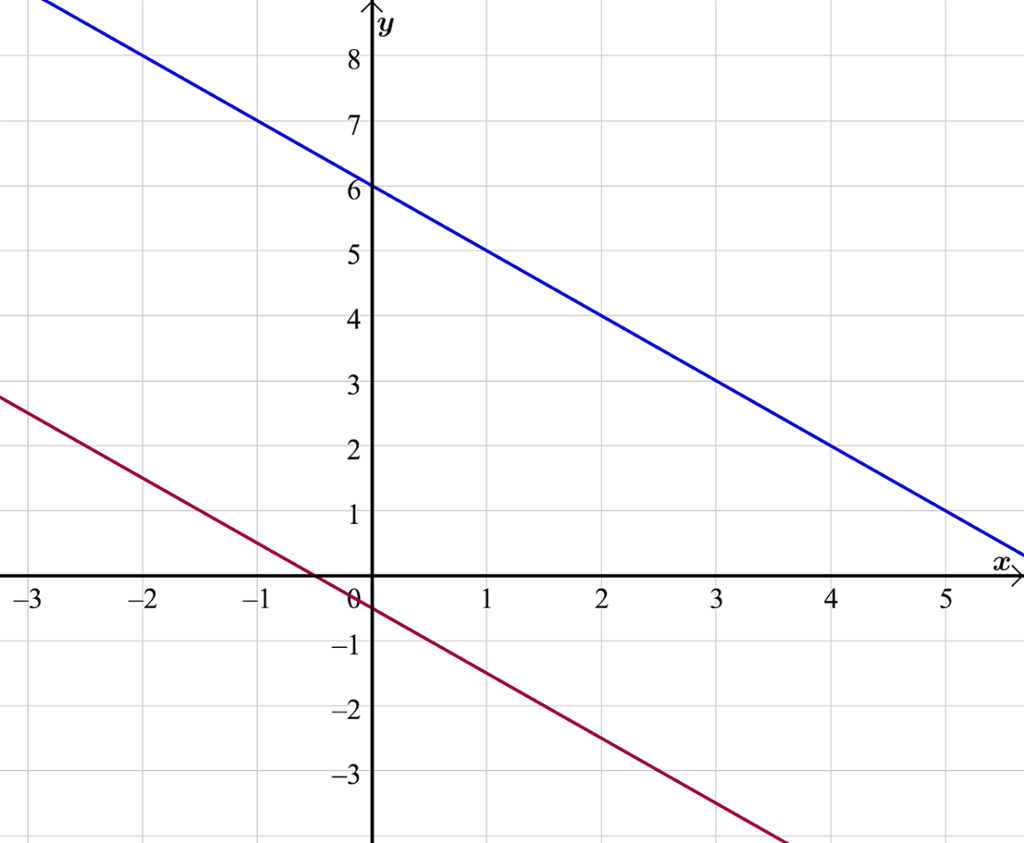
Siden linjene har samme stigningstall og ulikt konstantledd er de parallelle og vil ikke skjære hverandre. Likningssettet har ingen løsning.