Sektordiagram
La oss tenke oss at Mary Ann har gjennomført en undersøkelse og funnet at følgende karakterer ble gitt på en matematikkprøve:
4 2 5 3 3 2 5 4 1 3 2 2 5 3 1 4 2 5 3 2 4 3 6 2 5 3 2 5 5 4
Et sektordiagram egner seg spesielt godt til å vise hvor stor andel en verdi eller kategori i et tallmateriale utgjør i forhold til helheten.
Vi ser igjen på karakterfordelingen på matematikkprøven i klassen til Mary Ann.
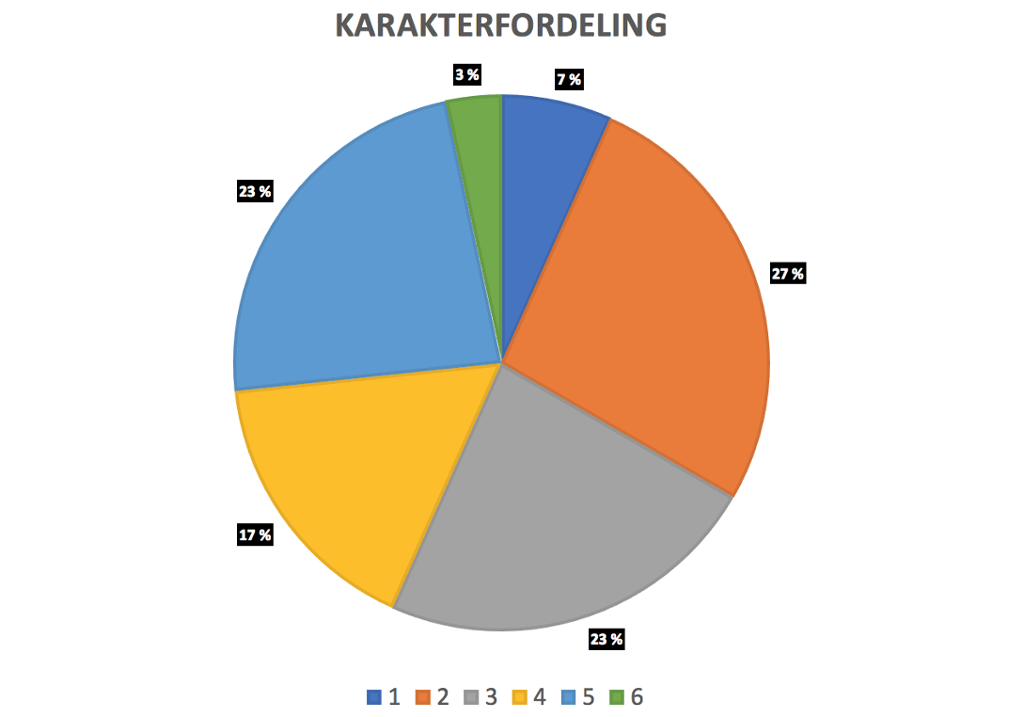
I regnearket Excel merker vi frekvenskolonnen og velger «Sett inn» og ønsket sektordiagram. Ved å velge «Utforming» kan vi finne fram til ønsket oppsett og format for diagrammet.
Arealet av hver sirkelsektor illustrerer andelen elever som har fått den aktuelle karakteren.
For å tegne et sektordiagram på papir trenger vi en passer og en gradskive. Før vi kan tegne, må vi gjøre noen beregninger.
Vi kan dele en sirkel inn i 360.
Siden det til sammen er 30 elever i klassen, må hver elev tilsvare av sirkelen.
Vi kan da sette opp følgende tabell:
Karakter | Frekvens | Grader |
|---|---|---|
1 | 2 | 2 · 12° = 24° |
2 | 8 | 8 · 12° = 96° |
3 | 7 | 7 · 12° = 84° |
4 | 5 | 5 · 12° = 60° |
5 | 7 | 7 · 12° = 84° |
6 | 1 | 1 · 12° = 12° |
Nå kan vi tegne en sirkel ved hjelp av en passer og bruke gradskiven til å avmerke størrelsen på sirkelsektorene.
Legg merke til at 1 % alltid svarer til .