Likningssett av første og andre grad
Da vi løste likningssett med to likninger av første grad, brukte vi innsettingsmetoden. Denne metoden kan vi også bruke her. Det lureste er da ofte å finne et uttrykk for den ene ukjente ved hjelp av førstegradslikningen, og så sette dette uttrykket inn i andregradslikningen.
Vi har gitt likningssettet
Vi bruker førstegradslikningen til å finne et uttrykk for
Vi setter så uttrykket for inn i andregradslikningen
Legg merke til at vi her dividerer med i siste linje for å få greiere tall å arbeide med når vi skal bruke abc-formelen.
Vi bruker abc-formelen til å løse denne likningen
Vi setter så disse løsningene inn i uttrykket for y
Likningssettet har to sett med løsninger
( eller,
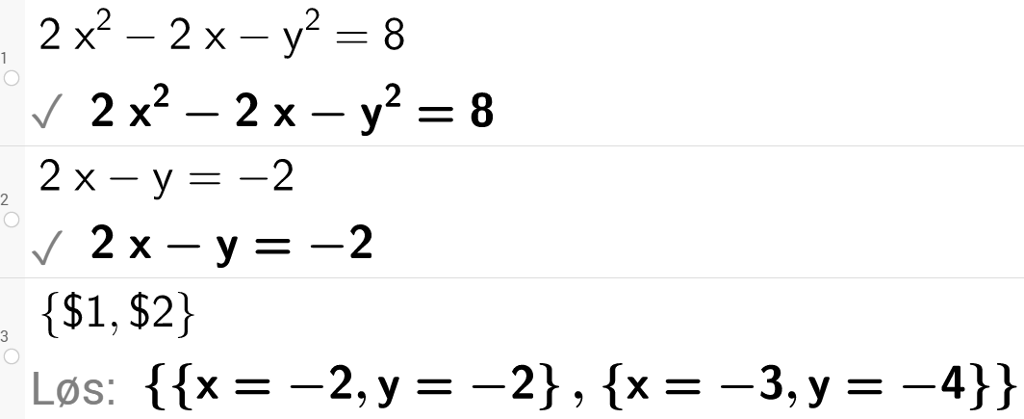
Vi kan løse likningen fra forrige eksempel i GeoGebra.
Du markerer rute 1 og 2 for deretter å bruke
I funksjonskapitlet skal du se hvordan vi kan løse likningssett grafisk.