Definisjonen av den deriverte
Vi benytter oss av samme prinsipp som vi brukte for å finne en tilnærmet verdi for den momentane vekstfarten.
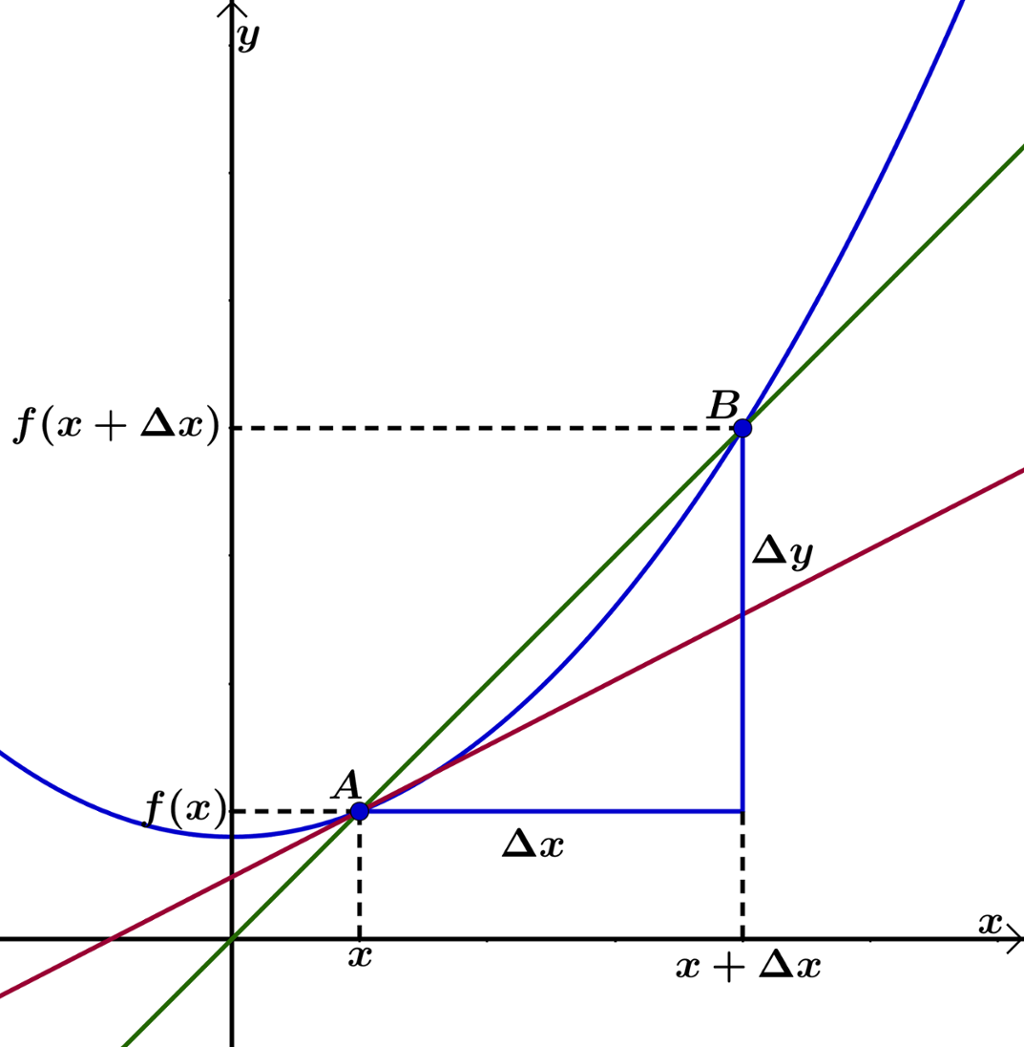
Vi tar utgangspunkt i en tilfeldig funksjon .
Vi tegner grafen til funksjonen, velger en tilfeldig -verdi og får et punkt på grafen .
Vi ønsker å finne vekstfarten til funksjonen for akkurat denne -verdien.
Vi gir et tillegg og får et nytt punkt på grafen, .
Vi trekker en sekant (grønn linje) gjennom punktene og .
Vi regner ut stigningstallet for denne linja:
Vi har da funnet et uttrykk for gjennomsnittlig vekstfart fra A til B.
Vi lar nå punktet nærme seg punktet . Vi lar altså gå mot null.
Da vil sekanten (grønn) gradvis nærme seg til å bli en tangent (rød linje) til kurven i .
Stigningstallet (brattheten) til denne tangenten forteller hvor fort kurven vokser akkurat her. Vi kaller dette stigningstallet for den momentane veksten i punktet eller den deriverte til i punktet. Vi skriver og leser «
Legg merke til at tegnet for den deriverte er en liten apostrof.
Den deriverte
Vi ser på grafen ovenfor.
nærmer seg mot når
Den deriverte i et punkt er stigningstallet til tangenten til grafen i dette punktet.
Den deriverte i et punkt og den momentane vekstfarten i punktet er det samme.
Definisjonen av den deriverte er en lokal definisjon. Den sier noe om verdien av den deriverte i et punkt, nemlig punktet med førstekoordinaten
Derivere betyr "å utlede eller avlede" og
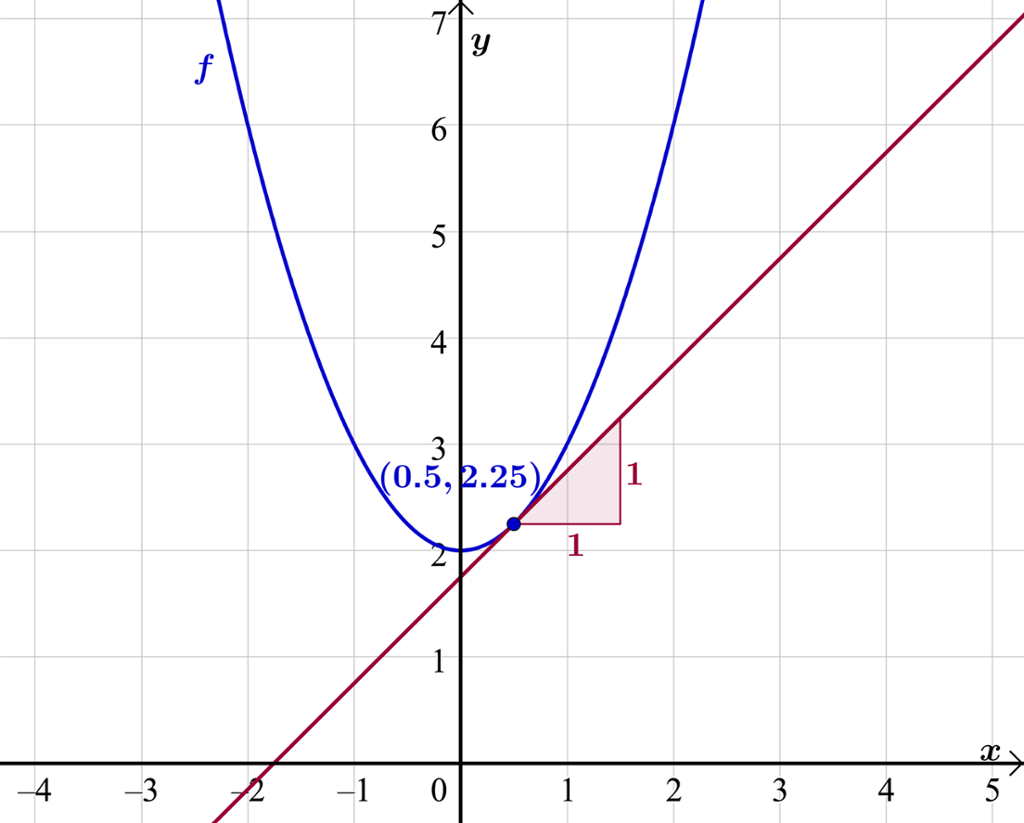
Den momentane vekstfarten eller den deriverte av
Vi kan finne en verdi for denne vekstfarten grafisk ved å tegne grafen til
Vi ser at tangenten har stigningstallet
Den deriverte av
Vi vil nå regne oss fram til den deriverte til
Vi husker at definisjonen på den deriverte
Hvordan finner vi så
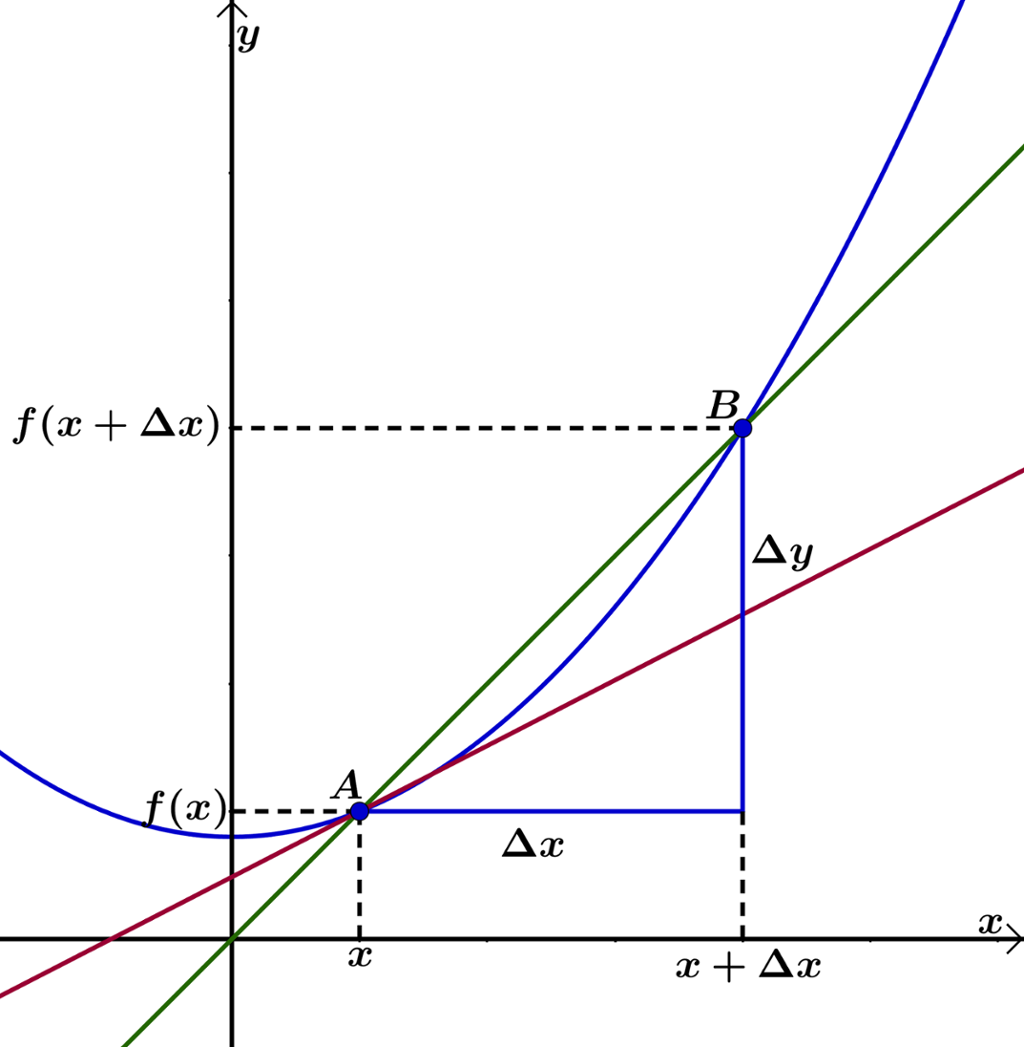
Det gir
(Husk at
Når
Vi har nå funnet at når
Da kan vi regne ut
Den deriverte funksjonen til
Vi kan bruke denne funksjonen til å finne den momentane vekstfarten for alle verdier av
For eksempel er