Modell for utgifter til leie av selskapslokaler
To firmaer leier ut selskapslokaler.
Firma A tar en fast leiepris på kroner og et timetillegg på kroner. Kostnadene i kroner, , ved leie av lokalet i timer kan beskrives med funksjonsuttrykket eller modellen
Firma B tar en fast leiepris på kroner og et timetillegg på kroner. Kostnadene i kroner, , ved leie av lokalet i timer kan beskrives med funksjonsuttrykket eller modellen
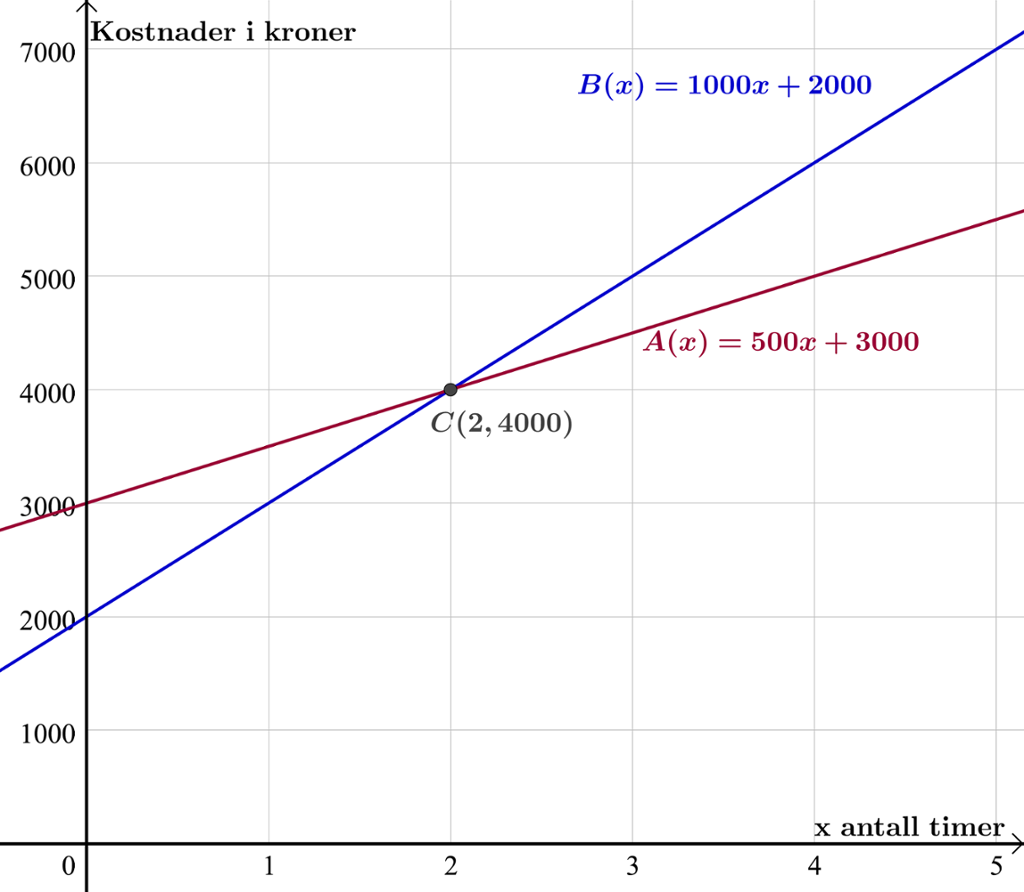
Vi tegner grafene til de to funksjonene og finner skjæringspunktet mellom grafene ved kommandoen «Skjæring mellom to objekt».
Grafene skjærer hverandre når . Det betyr at hvis du skal leie lokalene i to timer, er det prismessig det samme hvilket firma du velger. Prisen er kroner hos begge firmaene.
Hvis du skal leie lokalet i mindre enn to timer, lønner det seg å velge firma B. Det ser vi ved at grafen til ligger under grafen til i dette området.
Hvis du skal leie lokalet i mer enn to timer, lønner det seg å velge firma A. Det ser vi ved at grafen til ligger under grafen til i dette området.

Vi kan kontrollere den grafiske løsningen ved regning.
Vi får også her at leieprisene er like når leietiden er to timer og at leieprisen da er kroner.
Hos firma A er totalkostnadene i kroner ved leie av lokalet i timer gitt med funksjonsuttrykket
Konstantleddet er og viser her at den faste leieprisen er kroner . Den må betales uansett hvor mange timer lokalet leies. Legg merke til at grafen skjærer -aksen i punktet .
Stigningstallet er . Det betyr at det koster kroner for hver ekstra time lokalet leies.
Kostnadene øker jevnt med økningen i antall leide timer. Vi har lineær vekst i kostnadene.
Funksjonen gitt ved er strekningen i meter som er løpt etter minutter.
Her er konstantleddet lik null, og det viser at løpt strekning er null ved tida null. «Klokka» starter når løpeturen begynner.
Stigningstallet er . Det betyr det løpes meter for hvert ekstra minutt. Det forteller altså at farten er meter per minutt.
Antall løpte meter øker jevnt med økningen i antall minutter det løpes. Vi har lineær vekst i antall løpte meter.