Modell for omkretsen til en sirkel
Vi vil undersøke sammenhengen mellom radius til en sirkel og omkretsen av sirkelen.
For å samle inn data kan vi finne sirkelformede gjenstander og måle sammenhørende verdier av radius og omkrets, eller vi kan alternativt bruke GeoGebra til å finne noen sammenhørende verdier.
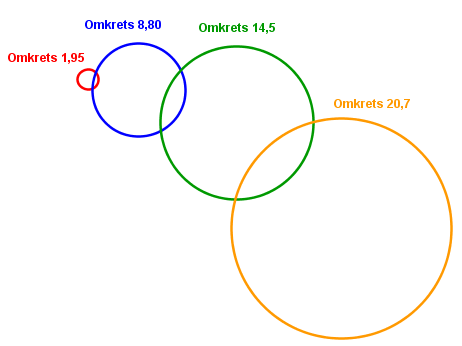
Bruk GeoGebra til å tegne fire sirkler med radius på henholdsvis 0,310 cm, 1,40 cm, 2,30 cm og 3,30 cm.
Bruk deretter "Avstand eller lengde"-knappen til å måle omkretsen av sirklene.
For hver verdi av radius, som vi kan kalle , får vi en verdi for omkretsen, som vi kan kalle . Vi sier at omkretsen er en funksjon av radius, .
Vi setter resultatene opp i en tabell.
Radius | 0,31 | 1,40 | 2,30 | 3,30 |
|---|---|---|---|---|
Omkrets | 1,95 | 8,80 | 14,45 | 20,73 |
Vi legger verdiene fra tabellen inn i regnearket i GeoGebra slik som vist på bildet under. Marker så de aktuelle rutene i regnearket og velg "Regresjonsanalyse".
De sammenhørende verdiene for radius og omkrets vises nå som punkter i et koordinatsystem. Det ser ut som om punktene ligger på ei rett linje.
Velg derfor "Lineær" som "Regresjonsmodell".
Vi har da funnet at er en matematisk modell for sammenhengen mellom radius og omkrets i en sirkel.
Vi ser at den rette linja passer godt med punktene.
Du har tidligere lært at formelen (modellen) for omkretsen av en sirkel er .
Hvordan stemmer resultatet vårt med dette?