Alternative metoder for å finne likningen til ei rett linje

Du får oppgitt at ei rett linje har stigningstall $a=2$ og går gjennom punktet $\left(1, -3\right)$ .

Finn likningen for linja.

Alternativ 1. Vi bruker ettpunktsformelen

Vi setter inn koordinatene til det oppgitte punktet og verdien for stigningstallet i ettpunktsformelen

$\begin{array}{rcl}& & \begin{array}{rcl}y-y_1& = & a\left(x-x_1\right)\\ & & \\ y-\left(-3\right)& =& 2\left(x-1\right)\\ & & \\ y+3& =& 2x-2\\ & & \\ y& =& 2x-5\end{array}\end{array}$

Vi har funnet likningen for linja.

Alternativ 2. Vi bruker at generell likning for ei rett linje er

$y=ax+b$

$a=2$ gir at likningen blir $y=2x+b$.

Punktet $\left(1, -3\right)$ ligger på linja og er derfor en løsning av likningen.

Vi setter inn i likningen og får

$\begin{array}{rcl}& & \begin{array}{rcl}-3& = & 2·1+b\\ & & \\ b& =& -3-2=-5\end{array}\end{array}$

Likningen for linja blir $y=2x-5$

Alternativ 3. Grafisk løsning

Avsett det kjente punktet i et koordinatsystem, enten for hånd eller digitalt. Bruk stigningstallet til å finne et nytt punkt på linja. Trekk linja gjennom punktene og les av hvor grafen skjærer $y$-aksen. Du har da funnet konstantleddet og dermed også likningen for linja.

Ei rett linje går gjennom punktene $\left(-2, -3\right)$ og $\left(1, 3\right)$.

Finn likningen for linja.

Alternativ 1. Vi bruker ettpunktsformelen

Vi finner først stigningstallet

$a=\frac{y_2-y_1}{x_2-x_1}=\frac{3-\left(-3\right)}{1-\left(-2\right)}=\frac{3+3}{1+2}=\frac{6}{3}=2$

Vi setter inn koordinatene til ett av de oppgitte punktene og verdien for stigningstallet i ettpunktsformelen. Vi kan velge hvilket som helst punkt bare det ligger på linja. Her har vi valgt punktet $$ \left(1, 3\right)$$.

$\begin{array}{rcl}& & \begin{array}{rcl}y-y_1 & = & a\left(x-x_1\right)\\ & & \\ y-3 & =& 2\left(x-1\right)\\ & & \\ y-3 & =& 2x-2\\ & & \\ y & =& 2x+1\end{array}\end{array}$

Vi har funnet likningen for linja.

Alternativ 2. Vi bruker at generell likning for ei rett linje er

$y=ax+b$

Siden punktene $\left(-2, -3\right)$ og $\left(1, 3\right)$ ligger på linja, må koordinatene til disse punktene passe i den generelle likningen $y=ax+b$.

Vi får et likningssett med to ukjente, $a$ og $b$

$\begin{array}{rcl}-3& =& a·\left(-2\right)+b\end{array}$ og $\begin{array}{rcl}3& =& a·1+b\end{array}$

Starter med den første likningen

$\begin{array}{rcl}-3& = & -2a+b\\ & & \\ b& =& -3+2a\end{array}$

Setter dette inn i den andre likningen

$\begin{array}{rcl}3& = & a·1+\left(-3+2a\right)\\ & & \\ 3& =& a-3+2a\\ & & \\ 3a& =& 6\\ & & \\ a& =& 2\end{array}$

Setter resultatet for $a$ inn i likningen for $b$

$\begin{array}{rcl}b& = & -3+2·2\\ & & \\ b& =& 1\end{array}$

Likningen for linja blir $y=2x+1$.

Alternativ 3. Grafisk løsning

Åpne bilde i et nytt vindu

CC BY-NC-SA

Bilde: Olav Kristensen

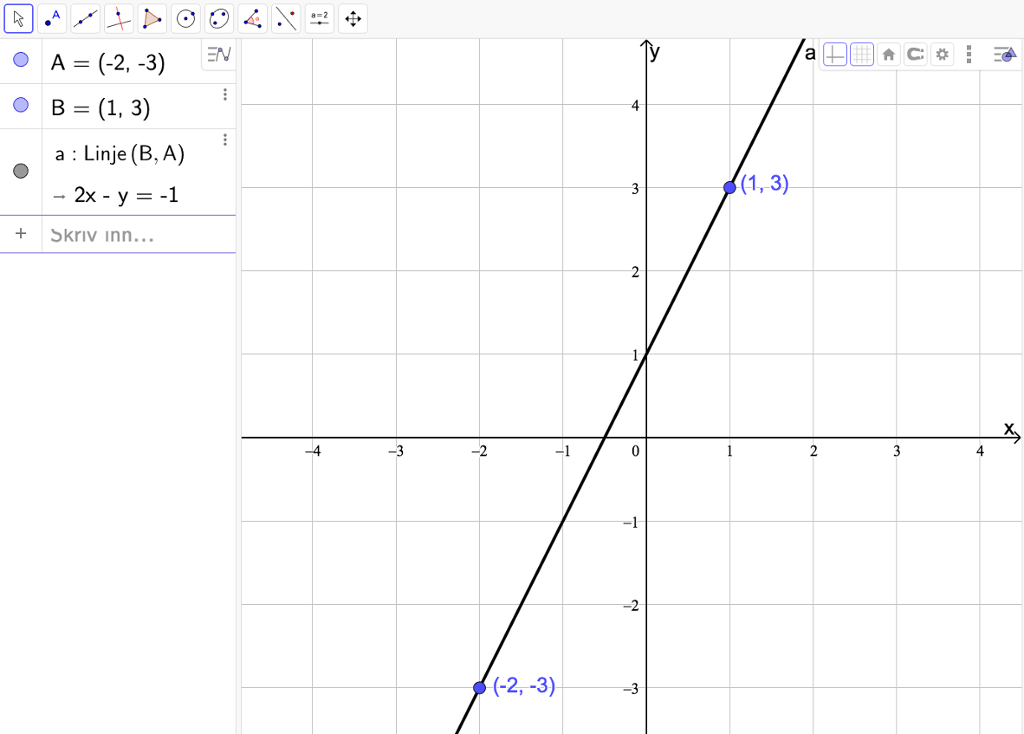
I GeoGebra markerer du punktene $\left(-2, -3\right)$ og $\left(1, 3\right)$ ved å klikke på knappen «Nytt punkt» eller ved å skrive inn punktene på skrivelinja. Klikk så på knappen «Linje» og deretter på de to punktene. Likningen for linja vises i algebrafeltet

I algebrafeltet på bildet vises likningen for linja på en litt uvant form. Høyreklikk da på likningen for linja og velg at likningen skal vises på formen $y=ax+b$.

CC BY-NC-SA

Bilde: Olav Kristensen

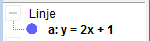
Du får at likningen for linja er $y=2x+1$.

Uten å bruke digitale hjelpemidler kan du avsette de kjente punktene i et koordinatsystem. Trekk ei rett linje gjennom punktene. Les av hvor linja skjærer $y$-aksen. Du har da funnet konstantleddet. Stigningstallet kan du finne ved å regne ut endring i $y$-verdi dividert med endring i $x$-verdi.