Matematiske modeller som grunnlag for beslutninger

Utviklingen av verdensrekorden for 500 meter på skøyter for herrer er gjengitt i tabellen nedenfor.
År | 1990 | 1992 | 1994 | 1996 | 1998 | 2001 | 2005 | 2007 |
|---|---|---|---|---|---|---|---|---|
Rekord i sekunder | 36,45 | 36,41 | 35,76 | 35,39 | 34,82 | 34,32 | 34,30 | 34,03 |
Vi lar være antall år etter 1990 og rekorden i sekunder. Så fremstiller vi opplysningene fra tabellen som punkter i et koordinatsystem.
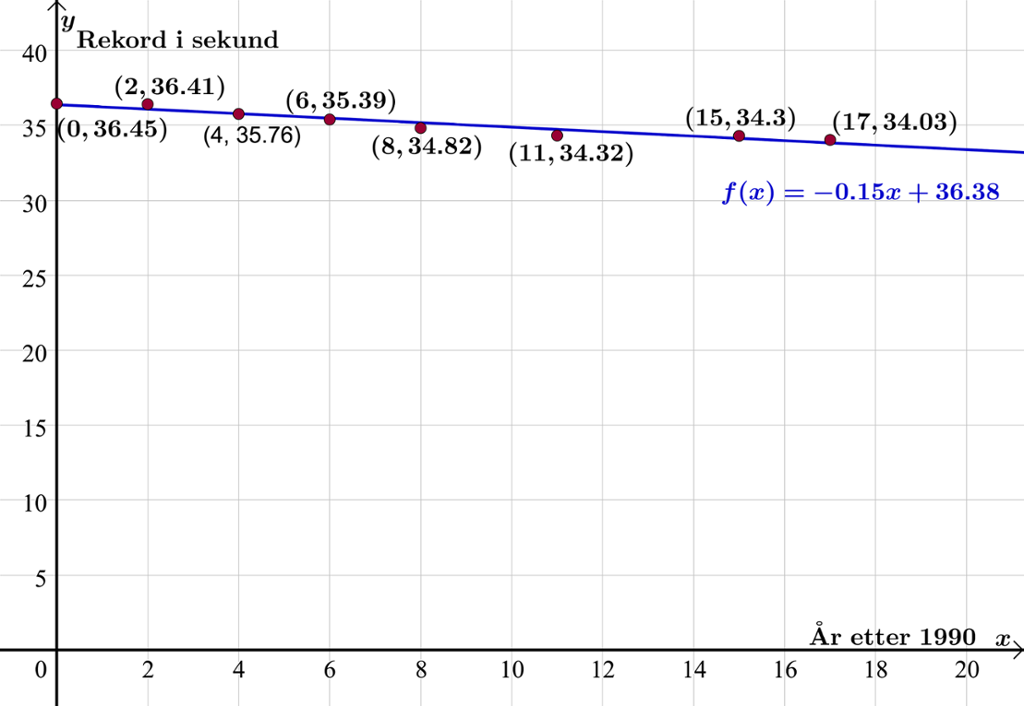
Punktene ligger tilsynelatende på en rett linje.
Vi bruker regresjon og finner en lineær funksjon som kan være modell for sammenhengen mellom rekorden og året den er satt
Grafen til funksjonen er tegnet i det samme koordinatsystemet.
Vi kan benytte modellen til å beregne hva verdensrekorden vil være i år 2090 dersom modellen gjelder.
Rekorden i 2090 vil etter modellen være 21,38 sekunder. Modellen er også representert med grafen til funksjonen.
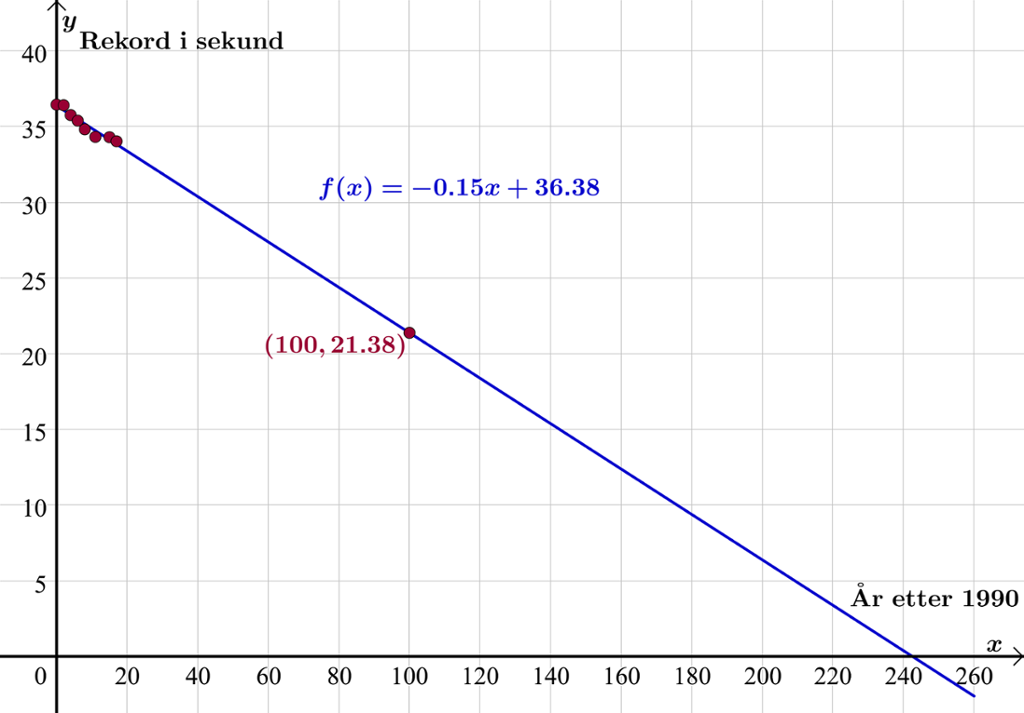
Grafen til modellen viser at rekorden på 500 m skøyter vil bli null i år 2230. Vi vet at dette er helt urealistisk, og det viser med all tydelighet hvor varsomme vi må være med å stole på matematiske modeller.
Utviklingen modellen ovenfor skisserer, er så usannsynlig at den ikke egner seg som grunnlag for beslutninger om framtidig utforming av skøytearenaer. Modellen egner seg muligens til å si noe om utviklingen noen få år fram i tid.
En annen modell som skisserer en mer sannsynlig utvikling, er gitt med potensfunksjonen
(Her er det første punktet tatt bort i regresjonen.)
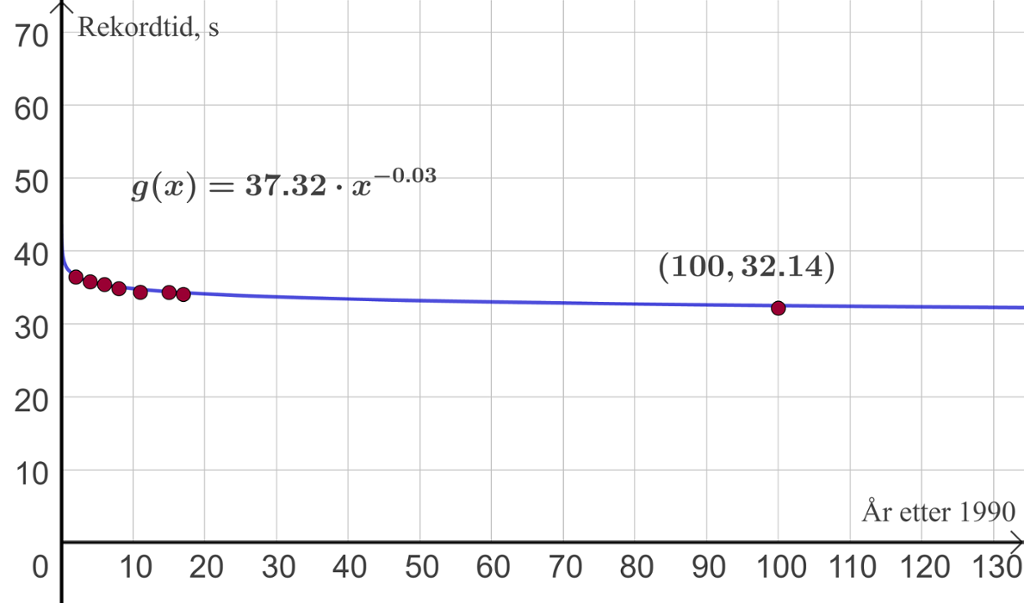
Modellen gir en rekord ned mot 32 sekunder i år 2090. Kanskje dette ikke er så urealistisk? Denne modellen er nok mer egnet som grunnlag for beslutninger om fremtidige skøyteanlegg.

20. november 2015 ble 34-grensen brutt da Pavel Kulizjnikov fra Russland satte ny verdensrekord i Salt Lake City med tiden 33,98 sekunder.
År 2015 er 25 år etter 1990. Regningen i CAS viser at av de to modellene fra 2007, er det
som stemmer best med resultatet fra 2015.