Generelt om rasjonale funksjoner
En rasjonal funksjon er en funksjon som kan skrives som en brøk der telleren og nevneren er polynomer.
Funksjonen gitt ved er en rasjonal funksjon.
En brøk er ikke definert når nevneren er lik null. Det betyr at ikke eksisterer. Grafen har ikke noe punkt for . Vi sier at grafen har et brudd for .
Vi tegner grafen til i GeoGebra og skriver også inn kommandoen Asymptote[f].
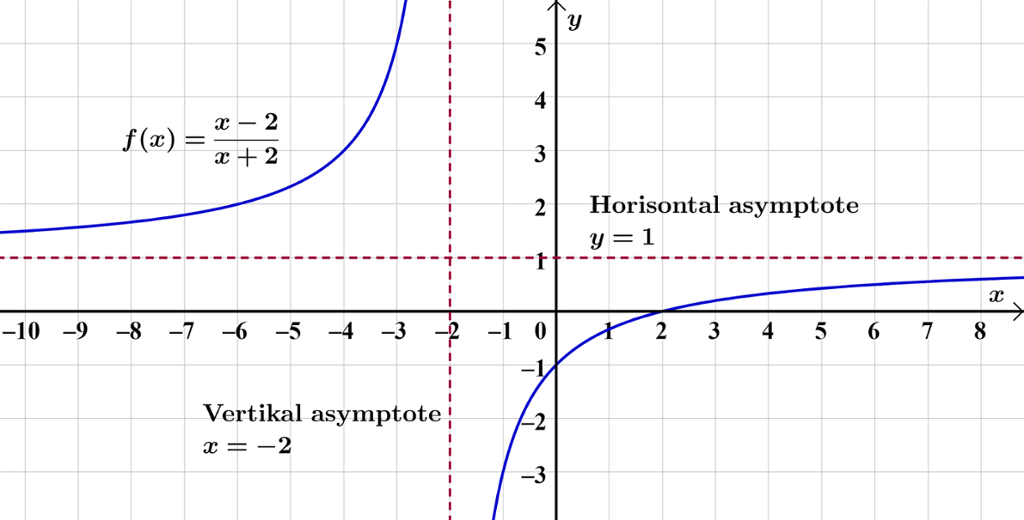
Legg merke til at grafen er symmetrisk om skjæringspunktet mellom asymptotene.
Når nærmer seg verdien fra venstre, ser du av grafen at funksjonsverdiene vokser over alle grenser.
Det kan vises at dette er riktig. Funksjonsverdiene nærmer seg ikke en bestemt verdi når nærmer seg verdien fra venstre, men blir uendelig store.
Vi skriver
når
Vi leser " går mot uendelig når går mot fra venstre".
Tilsvarende viser det seg at funksjonsverdiene synker mot minus uendelig når nærmer seg fra høyre. Vi skriver
når
Legg merke til og som markerer om nærmer seg fra venstre eller fra høyre.
Du kan undersøke om dette virker sannsynlig ved å sette inn verdier for som er veldig nær .
Grafen til består av to deler, en del til venstre for linja og en del til høyre for linja . Linja kalles en loddrett eller vertikal asymptote.
Det kan videre vises at grafen «flater ut» og nærmer seg linja når går mot pluss eller minus uendelig. Det vil si at funksjonsverdiene nærmer seg verdien som grenseverdi når går mot pluss eller minus uendelig, men uten noen gang å bli lik .
Den ene delen av grafen nærmer seg linja ovenfra og den andre delen nedenfra. De to delene av grafen vil aldri krysse linja. Linja er en vannrett eller horisontal asymptote.