Hvordan tegne grafen til en andregradsfunksjon uten bruk av digitale verktøy

Gitt andregradsfunksjonen $g\left(x\right)=x^2-4x+3 , D_g=\mathrm{ℝ}$

Vi starter med å finne symmetrilinje, bunnpunktet og eventuelle nullpunkter. (Hvordan kan vi se av funksjonsuttrykket at grafen til $g$ har et bunnpunkt?)

$\begin{array}{rcl} g\left(x\right)& = & 0\\ & & \\ x^2-4x+3& =& 0\\ & & \\ x& =& \frac{-\left(-4\right)\pm \sqrt{{\left(-4\right)}^2-4·1·3}}{2·1}\\ & & \\ x& =& \frac{4\pm \sqrt{4}}{2}=\frac{4\pm 2}{2}\end{array}$

Nullpunktene er

$x=\frac{4+2}{2}=3 \wedge x=\frac{4-2}{2}=1$

Symmetrilinjen er

$x=\frac{4}{2}=2$

Grafen har et bunnpunkt siden andregradsleddet er positivt. I bunnpunktet er

$x=2 \wedge y=g\left(2\right)=2^2-4·2+3=-1$

Det vil si at bunnpunktet er $\left(2,-1\right)$.

I tillegg viser funksjonsuttrykket at grafen skjærer $y$-aksen i punktet $(0, 3)$.

Informasjonen samles i en verditabell.

Vi har markert symmetrilinja og minimalverdien med en pil i tabellen over.

Vi regner ut $g\left(5\right)=5^2-4·5+3=8$.

På grunn av symmetri er $g\left(-1\right)=g\left(5\right)=8$ og $g\left(4\right)=g\left(0\right)=3$.

Det gir verditabellen:

Vi har nå tilstrekkelig med punkter og kan tegne grafen til $g$.

Åpne bilde i et nytt vindu

CC BY-NC-SA

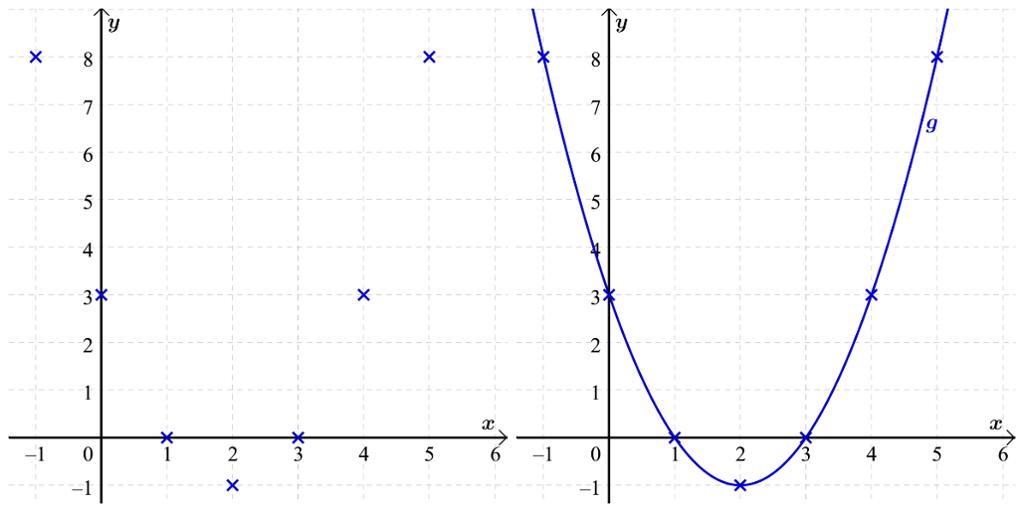
Bilde: Stein Aanensen, Olav Kristensen

Vi plotter punktene i et koordinatsystem og tegner en kurve gjennom punktene.