Det gylne snitt er en deling av en linje eller flate som oppleves som harmonisk. Komposisjonsprinsippet har vært brukt siden antikken. Det skaper en form for asymmetrisk balanse. Tredelsregelen går ut på det samme, men er en raskere og enklere metode.
Ildstedet er et blikkfang i interiøret og er plassert i krysningspunktet mellom vertikal og horisontal tredelslinje.
Tredelsregelen
Tredelsregelen og det gylne snitt
Poenget med størrelsesforhold er at helheten skal bli best mulig. De aller fleste nybegynnere plasserer elementer i midten, noe som gir et proporsjonalt forhold på 1:1. Dette gir et litt statisk uttrykk. For å skape mer energi i arbeidet kan du unngå midten og heller bruke tredelsregelen eller det gylne snitt.
Interiør plassert med utgangspunkt i tredelsregelen i utstillingen JOIN av Norwegian Presence.
Tredelsregelen
Dersom du tenker deg at du deler flaten i produktet eller arbeidet ditt i tre deler og , vil du få et rutenett med ni ruter. Du kan plassere et blikkfang, et hovedmotiv eller et element langs linjene eller i ett av de fire punktene der linjene krysser hverandre. Dette vil da gi et proporsjonalt forhold på 1:2.
I utstillingen av interiøret på bildet til høyre ser du at gulvflaten og den brune bakplaten ligger langs tredelslinjen både horisontalt og vertikalt. De tre bakerste møblene ligger langs den horisontale linjen, og elementet foran ligger i den vertikale linjen. Utstillingsdesigneren har ikke plassert møblene tilfeldig, men laget en dynamisk og spennende komposisjon ved å bruke tredelsregelen som virkemiddel.
Det gylne snitt
Det gylne snitt finner vi mange steder i naturen, for eksempel i sneglehuset.
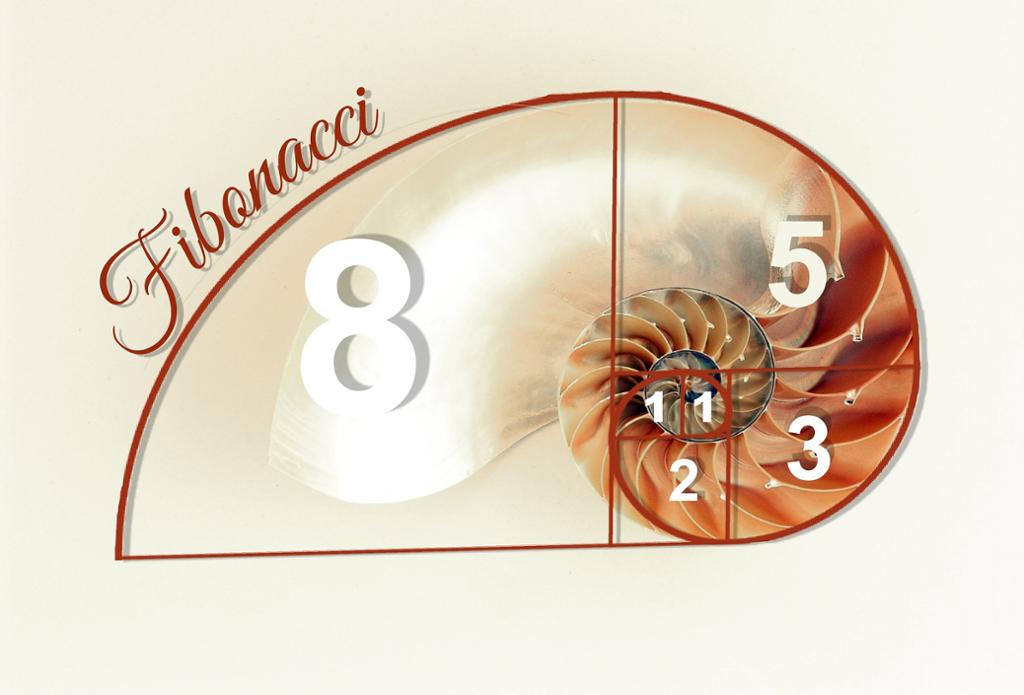
Det gylne snitt er et matematisk begrep som kan ligne litt på tredelsregelen. Forenklet kan vi dele en linje i åtte like store deler, og da finner vi det gylne snitt i det femte punktet. Det gylne snitt er et komposisjonsprinsipp som har vært brukt helt siden antikken. Det er denne inndelingen som oppleves som den mest harmoniske måten å dele en linje, flate eller form på. Vi finner inndelingen flere steder i naturen.
Fibonacci-tallene
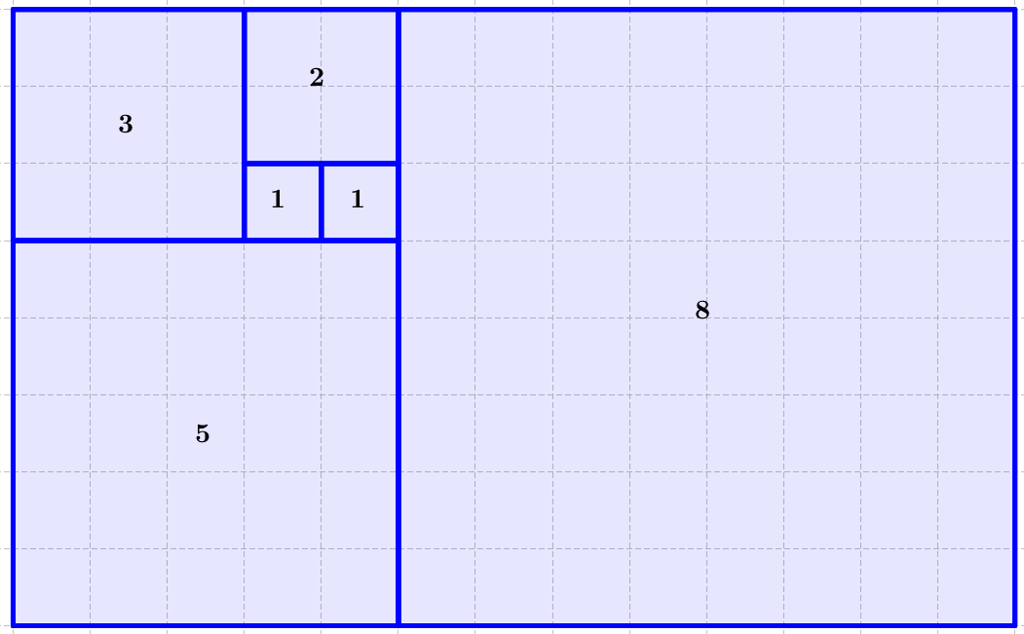
Det gylne snitt er vanlig å bruke i fotografering, ved at man plasserer motivet mot høyre eller venstre i bildeflaten. Like viktig er det å bruke prinsippene det gylne snitt eller tredelsregelen når du designer et tredimensjonalt produkt. Det kan for eksempel være når du plasserer en kontrast i en dekorasjon, eller det kan være størrelsesforholdet mellom skjebladet og skaftet i ei tresleiv.
Vil du vite mer?
Du kan lese mer om det gylne snitt på Matematikk.org, og på Numerologen.no kan du se hvordan tallet 9, spiralen, Fibonacci-rekka og det gylne snitt henger sammen.