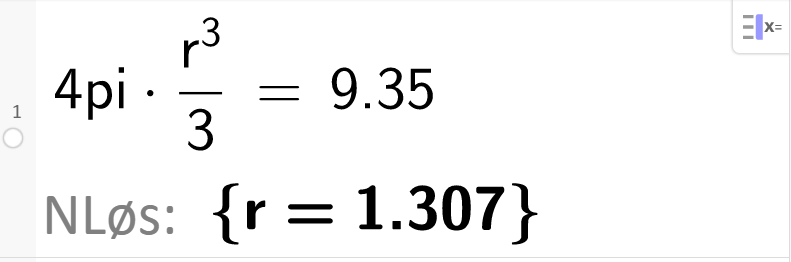Oppgave
Potenser og rotuttrykk
Oppgavene skal løses uten bruk av hjelpemidler med mindre det står noe annet. Nederst på siden kan du laste ned oppgavene som Word- og pdf-dokumenter.
Regn ut.
a)
b)
c)
Regn ut med hjelpemidler.
a)
b)
c)
Regn ut.
a)
b)
c)
d)
Regn ut.
a)
b)
c)
Vis at
a)
b)
Vis at
a)
b)
c)
d)
e)
Regn ut.
a)
b)
c)
d)
e)
f)
g)
Løs med CAS i GeoGebra.
Overflata til ei kule er gitt ved formelen
a) Regn ut radien i ei kule med ei overflate lik 17 cm².
Volumet til ei kule er gitt ved formelen
b) Regn ut radien i ei kule med et volum på 9,35 cm³.
Her kan du laste ned oppgavene som Word- og pdf-dokumenter.
Filer
- Potenser og rotuttrykk(DOCX)