Faktorisering av andregradsuttrykk ved hjelp av nullpunktmetoden
Vi ser på andregradsuttrykket .
Vi starter med å finne nullpunktene.
Vi løser da likningen .
Uttrykket er altså lik null når og når .
Ser du at uttrykket også er lik null når og når ?
Vi multipliserer og ser at
Vi har da at
Andregradsuttrykket er faktorisert!
Er dette en metode vi kan bruke for å faktorisere alle andregradsuttrykk?
Vi prøver med et nytt eksempel!
Vi ser på uttrykket .
Vi starter igjen med å finne nullpunktene, og løser likningen .
Uttrykket er altså lik null når og når .
Vi prøver samme metode som i forrige eksempel og ser at uttrykket også er lik null når og når .
Vi multipliserer og får
Dette er ikke det samme andregradsuttrykket som vi startet med.
Vi startet med
Når vi multipliserer ut parentesene, får vi
Ser du at vi kan multiplisere det siste uttrykket med , og få det andregradsuttrykket vi startet med?
Vi har da at
Andregradsuttrykket er faktorisert!
Hvis vi ønsker et uttrykk uten brøk, kan vi multiplisere 2-tallet inn i den siste parentesen
Vi ser fort at vi må multiplisere med , fordi det siste uttrykket inneholder leddet , mens det polynomet vi startet med, inneholder leddet .
Den metoden vi har brukt for å faktorisere i de to eksemplene ovenfor, kalles nullpunktmetoden. Du skjønner kanskje hvorfor?
Nullpunktmetoden
der og er løsningene av den generelle andregradslikningen
Bevis at nullpunktmetoden gjelder generelt ved å vise at
Når det bare finnes én løsning av andregradslikningen, er .
Når andregradslikningen ikke har løsninger, kan ikke uttrykket faktoriseres.
Vi faktoriserer uttrykket i eksempel 2 ved CAS i GeoGebra.
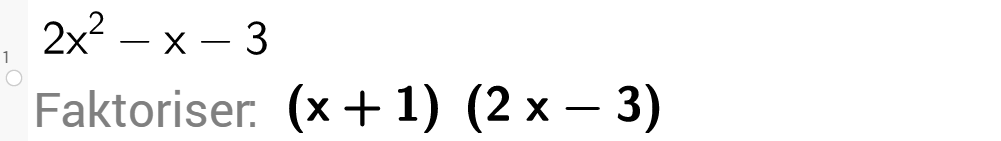
Ikke glem at må være med i det faktoriserte uttrykket! Hvor er det blitt av tallet foran parentesene når vi bruker CAS til å faktorisere uttrykket i eksempel 2?