Nullpunkter, toppunkter, bunnpunkter og symmetrilinje
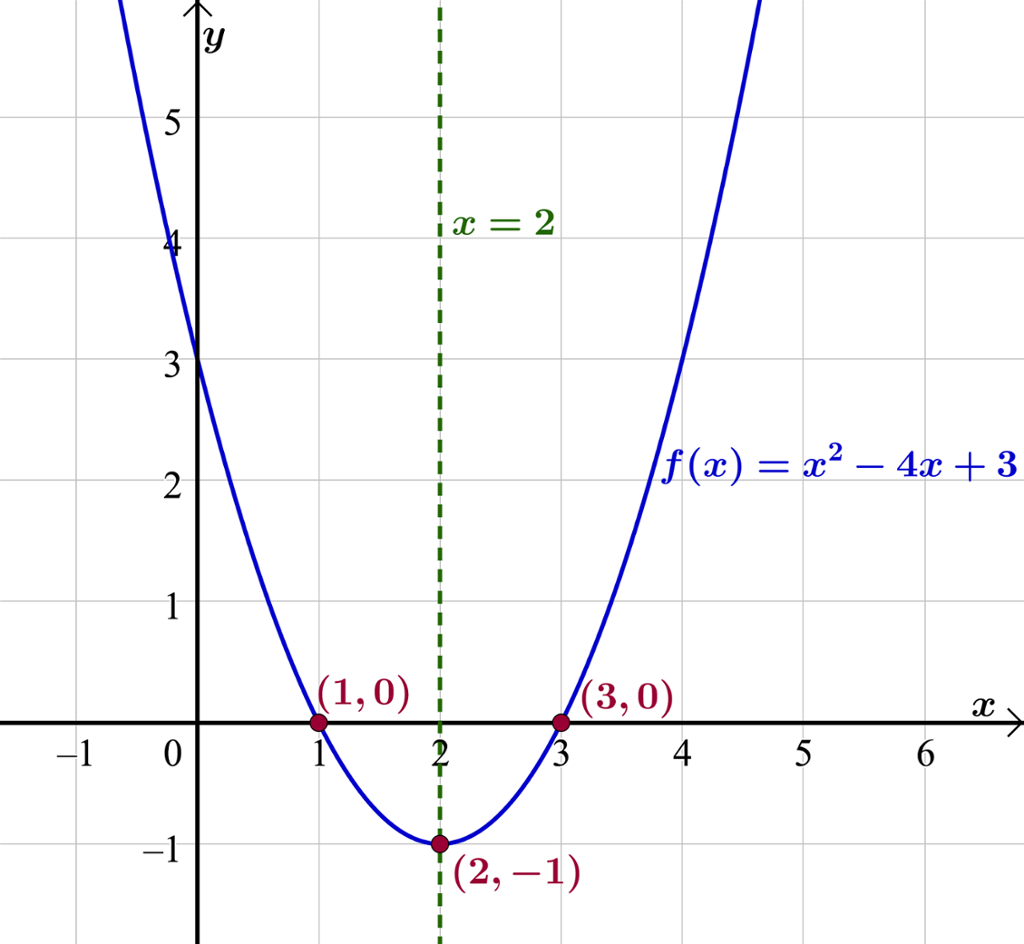
Vi tegner grafen til funksjonen i GeoGebra og finner nullpunktene med kommandoen «Nullpunkt[f]».
Grafen har et bunnpunkt, siden andregradsleddet er positivt. Vi finner bunnpunktet med kommandoen «Ekstremalpunkt[f]». Grafen har bunnpunkt .
I koordinatsystemet har vi tegnet inn symmetrilinja til , linja .
Vi ser at bunnpunktet ligger på symmetrilinja. Symmetrilinja ligger også like langt fra hvert av parabelens nullpunkter.
Vi har sett at vi kan finne parabelens nullpunkter ved å løse likningen .
Hvis vi stopper der, ser vi at .
De to nullpunktene ligger like langt fra parabelens symmetrilinje.
Det betyr at de to nullpunktene ligger like langt fra linja , og denne linja er altså parabelens symmetrilinje.
Generelt er nullpunktene gitt ved
Det betyr at vi kan finne symmetrilinja og -koordinaten til topp- eller bunnpunktet ved å «fjerne» kvadratroten i uttrykket vi får når vi setter .
Gitt andregradsfunksjonen
Vi finner nullpunktene ved å løse likningen . Det gir
Vi finner symmetrilinja og x-koordinaten til topp- eller bunnpunktet ved
Det betyr at vi kan finne mye informasjon om grafen til en andregradsfunksjon ved enkel regning uten å bruke digitale hjelpemidler.
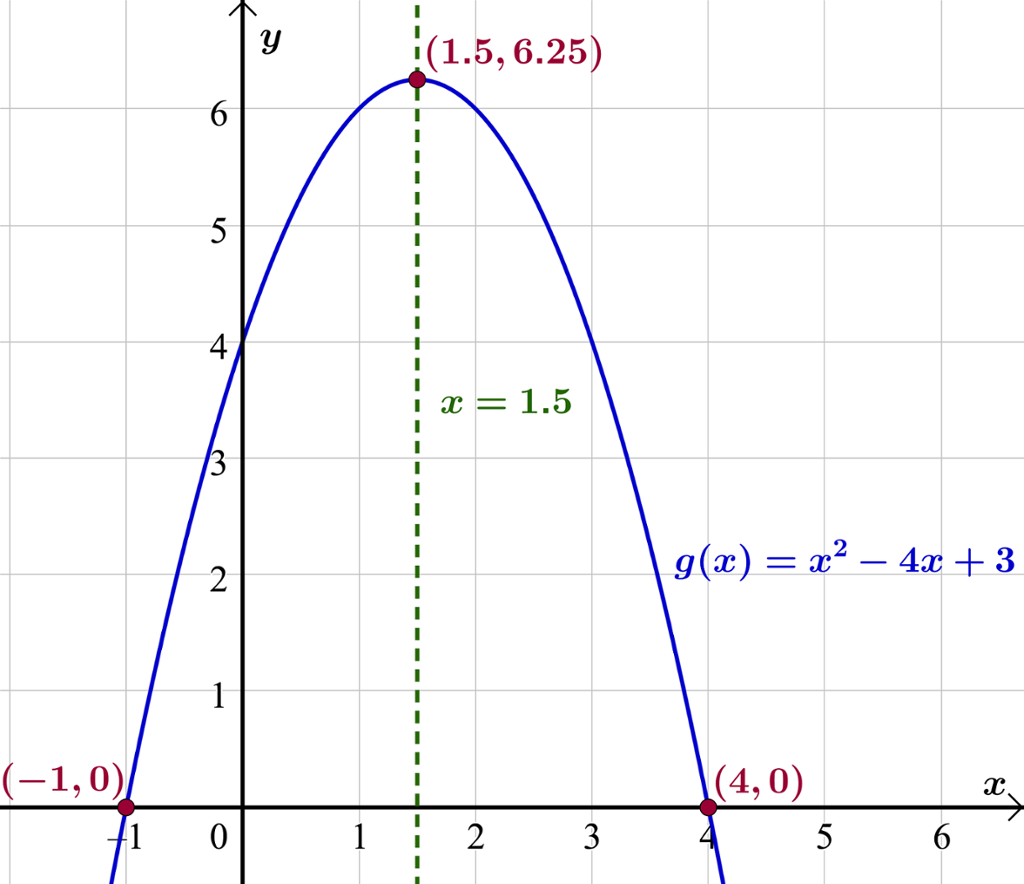
Gitt funksjonen . Finn nullpunktene til funksjonen.
Nullpunktene er og .
Symmetrilinja er
Vi ser at dette er -verdien midt mellom og .
Grafen har et toppunkt, siden andregradsleddet er negativt.
Toppunktet har koordinatene
Gitt funksjonen .
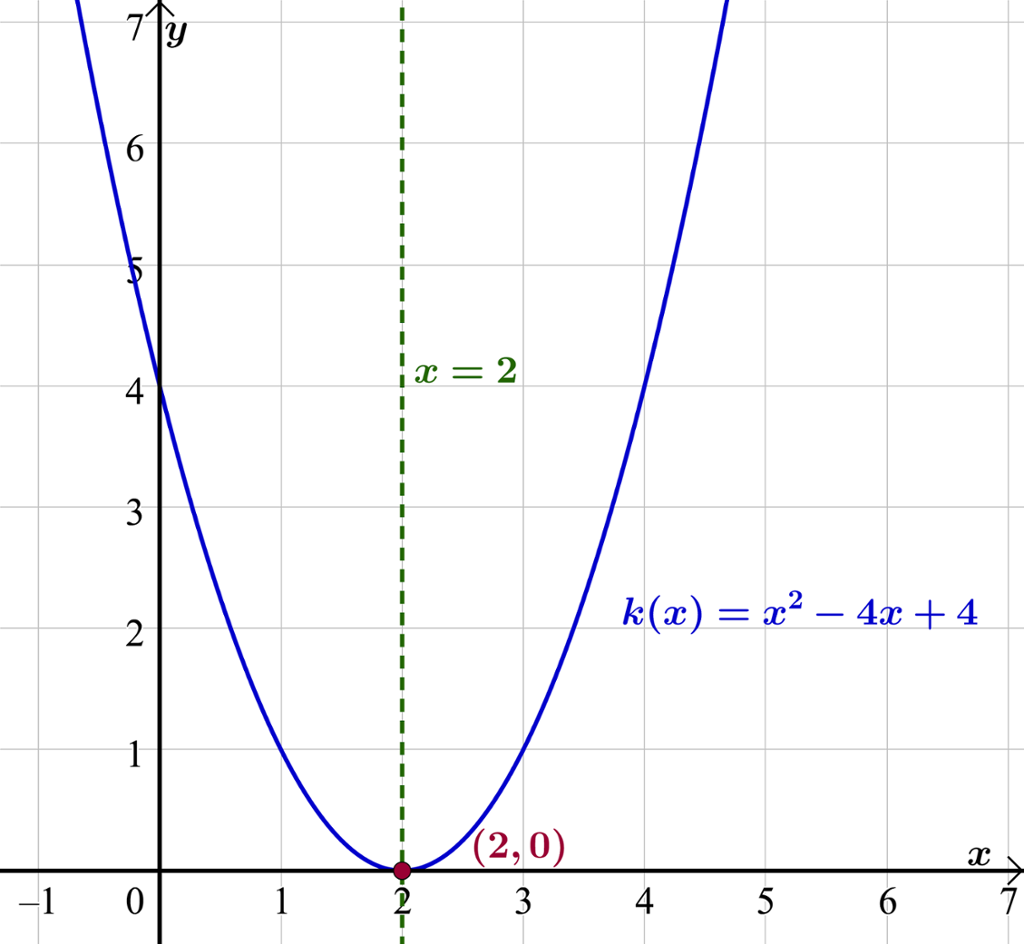
Finn eventuelle nullpunkter til funksjonen.
Nullpunktet er .
Vi får bare ett nullpunkt, siden uttrykket under kvadratroten blir lik null.
Symmetrilinja er gitt ved
Grafen har et bunnpunkt, siden andregradsleddet er positivt. Nullpunktet faller sammen med bunnpunktet og ligger på symmetrilinja.
Vi vet at . Bunnpunktet har koordinatene .
Gitt funksjonen .
Finn eventuelle nullpunkter til funksjonen.
Vi får et negativt tall under rottegnet. Likningen har ingen løsning. Det betyr at funksjonen ikke har nullpunkter, og grafen til funksjonen krysser aldri -aksen.
Siden konstantleddet , vet vi at grafen skjærer -aksen i punktet . Dette punktet ligger over -aksen. Grafen ligger da over -aksen for alle verdier av .
Vi finner symmetrilinja ved
Grafen har et bunnpunkt, siden andregradsleddet er positivt.
Bunnpunktet har koordinatene .