Tall og tallmengder

De første tallene du lærte som barn var sannsynligvis tallene

$1, 2, 3, 4,...$

Dette var også de første tallene menneskene tok i bruk.

Vi kaller disse tallene for de naturlige tallene. Mengden av alle de naturlige tallene symboliseres med bokstaven $\mathbb{N}$.

Vi skriver

$\mathbb{N}=\left\{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ...\right\}$

og leser «N er lik mengden av tallene $1, 2, 3, 4, 5,$ osv». Vi bruker mengdeparenteser for å liste opp en mengde av enkelttall. Prikkene etter $10$-tallet viser at tallene fortsetter i samme mønster, $11,12$ osv.

De naturlig tallene kan brukes til å beskrive et antall, for eksempel hvor mange epler du har. De kan også brukes til å angi en nummerrekkefølge, for eksempel resultatlisten ved en idrettskonkurranse.

Den tyske matematikeren Leopold Kronecker $(1823-1891)$ skal en gang ha sagt at «Gud skapte de naturlige tallene, resten er menneskets verk».

La oss tenke oss at du dyrker og selger epler. Hvis du har $8$ epler og selger $2$ epler, har du $6$ epler igjen. Dette kan illustreres med regneoperasjonen subtraksjon.

$8-2=6$

Vi subtraherer et naturlig tall fra et annet naturlig tall og får et nytt naturlig tall.

Men hva hvis kunden ønsker å kjøpe $8$ epler, eller til og med $12$ epler slik at du må låne $4$ epler av naboen?

Regnestykkene blir nå

$8-8 \mathrm{og} 8-12$

Her har vi ikke naturlige tall som gir svar på regneoperasjonene. Det er da matematikere har funnet på å utvide tallmengden med tallet 0 og de negative tallene, og vi får at

$8-8=0 \mathrm{og} 8-12=-4$

Null epler betyr at du ikke har flere epler, og $-4$ epler betyr at du skylder $4$ epler.

Vi utvider mengden av de naturlige tallene ved å plassere $0$ til venstre for $1$, $-1$ til venstre for $0$, $-2$ til venstre for $-1$ og så videre.

$\left\{..., -2, -1, 0, 1, 2,...\right\}$

Tallet $-1$ kan med fordel leses som «negativ $1$» for å markere at her brukes minustegnet som et fortegn, det forteller at tallet er negativt, og ikke som regnetegnet subtraksjon.

Den tallmengden vi nå har fått kalles for hele tall og symboliseres med $\mathbb{Z}$.

$\mathbb{Z}=\left\{..., -2, -1, 0, 1, 2,... \right\}$

Når vi bruker regneoperasjonene addisjon og subtraksjon på to hele tall, får vi alltid et nytt helt tall som resultat.

En tallinje kan gi et bilde av de hele tallene

Tall som ligger på hver sin side av tallet $0$, og like langt fra $0$, kalles for motsatte tall. For eksempel er $2$ og $-2$ motsatte av hverandre. Summen av et tall og det motsatte tallet er alltid lik null. Tallet $0$ er sitt eget motsatte tall.

De negative tallene ble ikke innført i Europa før på $1500$-tallet. Det var store diskusjoner før de ble godtatt. Både filosofer og teologer hadde store betenkeligheter med å godta negative tall.

Tallet $0$ ble godtatt i Europa noen hundre år tidligere. Noen matematikere regner tallet $0$ med blant de naturlige tallene, mens andre ikke gjør det. (Det er faktisk ingen som er gitt myndighet til å bestemme for eksempel om tallet $0$ skal regnes som et naturlig tall eller ikke!)

Når vi legger sammen, trekker fra hverandre og multipliserer hele tall, blir resultatet alltid et helt tall. Det er slik en matematiker liker å ha det. Én tallmengde og én regneoperasjon! Regneoperasjonen virker på tall i tallmengden og gir et nytt tall i tallmengden.

Når vi adderer et positivt tall, flytter vi oss til høyre på tallinjen. Adderer vi det positive tallet $2$, flytter vi oss to plasser til høyre på tallinjen, uansett om vi adderer tallet $2$ til et positivt eller negativt tall.

Når vi subtraherer et positivt tall, flytter vi oss til venstre på tallinjen. Subtraherer vi det positive tallet $2$, flytter vi oss to plasser til venstre på tallinjen. Hvis vi subtraherer det positive tallet $9$, flytter vi oss ni plasser til venstre på tallinjen.

Men hva vil det si å addere eller subtrahere negative tall?

Hvor havner vi på tallinjen hvis vi til tallet $2$ adderer det negative tallet $-5$, eller til tallet $3$ subtraherer det negative tallet $-4$?

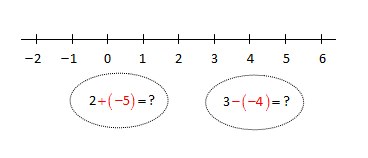
Hva vil det egentlig si å addere og subtrahere negative tall? Har vi praktiske situasjoner hvor vi kan få en forståelse av hva det vil si? Dette kommer vi tilbake til i Å regne med negative tall!