Andregradslikninger uten formel
En likning som kan skrives på formen der
Et eksempel på en andregradslikning er
Et annet eksempel er
🤔 Tenk over: Hva er koeffisientene a, b og c i denne likningen?
En andregradslikning inneholder alltid andregradsleddet, men førstegradsleddet og konstantleddet kan mangle, det vil si at b og/eller c kan være lik 0. Vi skal se på hvordan vi kan løse andregradslikninger på ulike måter.
Hvis
Vi ser på et eksempel der vi må ordne likningen før vi kan løse den:
🤔 Tenk over: Hva skjer hvis vi får et negativt tall på høyresiden av den ordnede likningen, for eksempel
Vi vet at dersom et produkt av to (eller flere) faktorer skal kunne bli 0, må minst én av faktorene være 0. Hvis vi kan faktorisere likningen vår slik at vi har to lineære faktorer på venstre side og 0 på høyre, betyr det at vi kan splitte likningen i to lineære likninger. For eksempel kan likningen
Når konstantleddet mangler
Når konstantleddet
Vi bruker at minst én av faktorene må være 0 for at produktet skal bli 0. Vi får dermed to løsninger, enten er
Stirremetoden
Hvis vi kan forkorte bort koeffisienten til
Noen andregradslikninger kan ordnes slik at vi får et fullstendig kvadrat på venstresiden og et tall på høyresiden.
🤔 Tenk over: Husker du hva et fullstendig kvadrat er?
La oss først se på likningen
Hvis vi omformer en andregradslikning slik at det til venstre for likhetstegnet står et fullstendig kvadrat, kan vi løse likningen på denne måten.
Husker du hvordan vi lagde fullstendige kvadrater da vi faktoriserte andregradsuttrykk? Hvis ikke kan du friske opp hukommelsen i artikkelen "Fullstendige kvadraters metode". Vi bruker samme metode nå, med en liten forskjell. Da vi faktoriserte uttrykk ved hjelp av denne metoden, la vi til og trakk fra kvadratleddet. Her har vi en likning, så vi kan heller velge å addere kvadratleddet på begge sider av likhetstegnet.
Vi vil løse likningen
Vi begynner med å ordne likningen slik at vi får leddene som inneholder x, på venstre side og konstantleddet på venstre side, og vi får også forkortet bort a:
Vi ønsker å få venstresiden på formen
Vi må finne ut hvilket tall vi må legge til på venstre side for å fullføre kvadratet. Vi setter
Vi legger nå til 4 på begge sider av likningen, bruker andre kvadratsetning til å faktorisere venstre side og løser likningen:
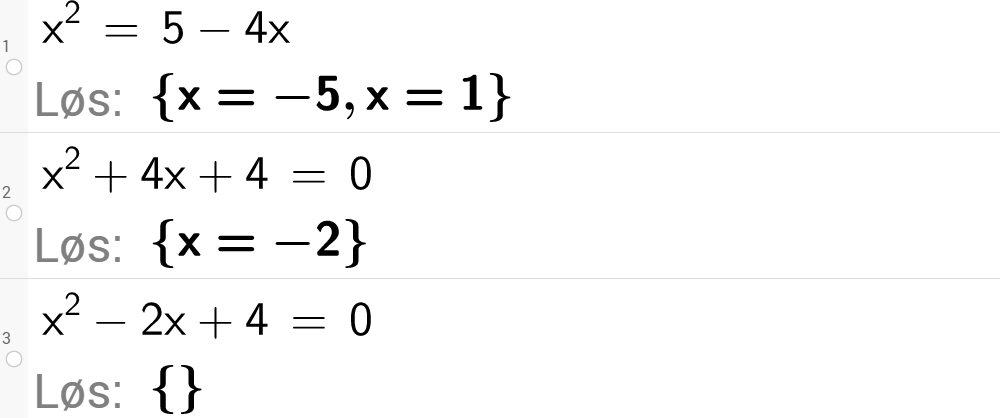
Når vi bruker CAS i GeoGebra, får vi løsningene enten ved å bruke kommandoen "Løs" eller ved å bruke knappen
Legg merke til at vi får en tom mengde når likningen ikke har noen løsning, slik som i linje 3.