Skjæringspunkt og nullpunkt

I skjæringspunktet mellom grafene til to funksjoner har begge funksjonene samme verdi for $$x$$ og samme verdi for $$y$$. Skal vi finne skjæringspunktet ved regning, setter vi derfor funksjonsuttrykkene lik hverandre og løser likningen vi da får.

Funksjonene $$f$$ og $$g$$ er gitt ved $$f\left(x\right)=2x-1$$ og $$g\left(x\right)=-x+2$$.

Finn skjæringspunktet mellom de to linjene grafisk og ved regning.

Grafisk løsning

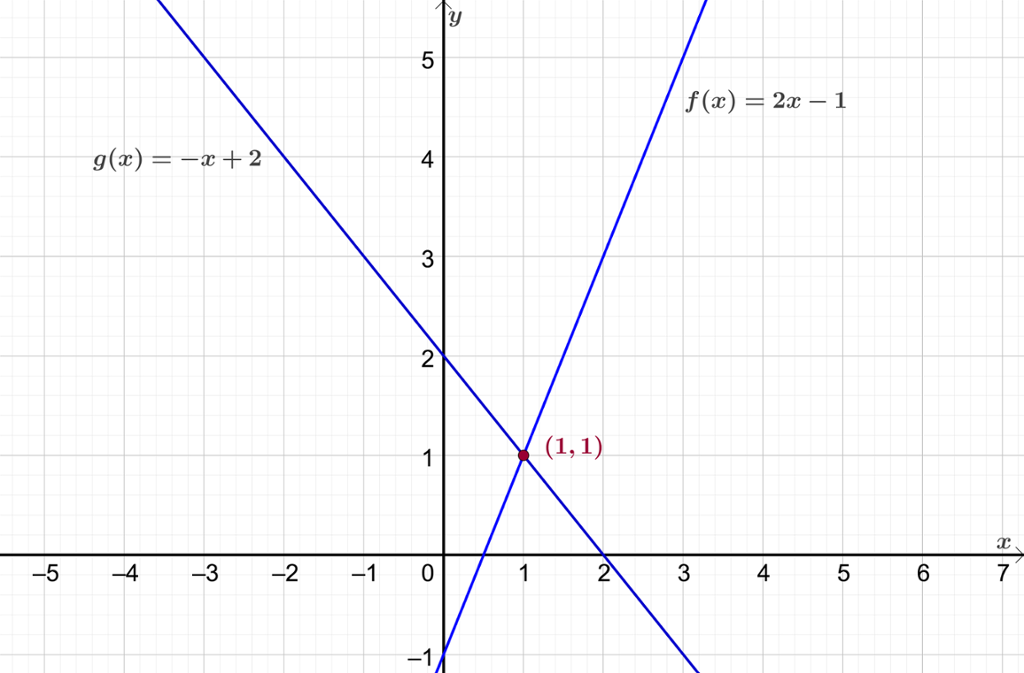
Vi tegner de to linjene i et koordinatsystem, leser av og finner at linjene skjærer hverandre i punktet $$\left(1, 1\right)$$.

I GeoGebra kan du bruke kommandoen «Skjæring[f,g]»,, eller knappen «Skjæring mellom to objekt».

Ved regning

Definisjon

Gitt funksjonen $$f\left(x\right)=2x-1$$.

$$\begin{array}{rcl}f\left(x\right)& =& 0\\ 2x-1& =& 0\\ x& =& \frac{1}{2}\end{array}$$

Nullpunktet til $$f$$ er $$x=\frac{1}{2}$$.

Gitt funksjonen $$g\left(x\right)=-x+2$$.

$$\begin{array}{rcl}g\left(x\right)& =& 0\\ -x+2& =& 0\\ -x& =& -2\\ x& =& 2\end{array}$$

Nullpunktet til $$g$$ er $$x=2$$.

I GeoGebra finner du nullpunkter enklest med verktøyet Nullpunkt, som ligger under den andre knappen på knapperaden øverst. Du kan også skrive kommandoen "Nullpunkt[ Polynom ]". Hvis funksjonen ikke er et polynom, brukes kommandoen "NullpunktIntervall[ Funksjon, Startverdi a, Sluttverdi b ]". Vi må altså legge inn det intervallet der vi finner nullpunktet (-ene). For andre funksjoner enn polynomer garanteres det ikke at GeoGebra finner alle nullpunktene til funksjonene.