Introduksjon til andregradsfunksjoner som modeller
I lineære funksjoner opptrer variabelen bare i første potens. En andregradsfunksjon har i tillegg et ledd hvor variabelen opptrer i andre potens. Det vil si at vi har ledd som inneholder . En andregradsfunksjon har ikke ledd med høyere potens av enn 2.
Gå sammen med noen medelever og bruk et tau som er litt over 12 meter langt. Bind sammen endene og form tauet til et rektangel som figuren viser. Omkretsen til rektangelet skal være 12 meter.
I et rektangel er to og to sider er like lange, slik at vi bare har to forskjellige sidelengder. Vi kaller disse for henholdsvis grunnlinje og høyde her.
La først grunnlinja være 1 meter. Lag et rektangel av tauet og mål lengden av høyden. Regn ut arealet av rektangelet.
Lag en verditabell der dere noterer resultatene av målingene og utregningen.
Gjør så det samme flere ganger, men varier lengden på grunnlinja til henholdsvis 2 meter, 3 meter, 4 meter, 5 meter og til slutt 6 meter.
Før alle resultatene inn i samme verditabell.
Plott så resultatene i et koordinatsystem der dere på -aksen avsetter lengden av grunnlinja og på -aksen avsetter arealene. Skisser en kurve gjennom punktene.
Hvor lang må grunnlinja være for å få størst areal?
La nå grunnlinja være meter.
- Kan dere finne en formel for høyden?
- Kan dere så finne en formel for arealet som funksjon av grunnlinja, ?
- Bruk GeoGebra og tegn grafen som viser arealet som funksjon av grunnlinja, .
- Plott inn punktene fra verditabellen i samme koordinatsystem. Hva ser dere?
- Sammenlign denne grafen med den grafen dere skisserte. Hva finner dere?
- Hva er det maksimale arealet firkanten kan få?
- Hva forteller grafens skjæringspunkter med -aksen?
Løsning
For hver verdi av får vi et bestemt rektangel med et bestemt areal. Vi har altså at arealet til rektangelet er en funksjon av . Omkretsen til rektangelet er 12 meter. To og to sider er like lange, slik at vi bare har to forskjellige sidelengder. Vi kaller disse for henholdsvis grunnlinje og høyde. Grunnlinja og høyden må til sammen være halve omkretsen, slik at når grunnlinja er , så må høyden være .
Formelen, modellen, for arealet som funksjon av grunnlinja blir da
Vi har en andregradsfunksjon.
Her er funksjonen representert ved en verditabell:
Grunnlinja i meter | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
Høyden i meter | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
Areal av rektangel i m2 | 0 | 5 | 8 | 9 | 8 | 5 | 0 |
I nederste linje har vi beregnet arealet av rektangelet for de forskjellige verdiene av .
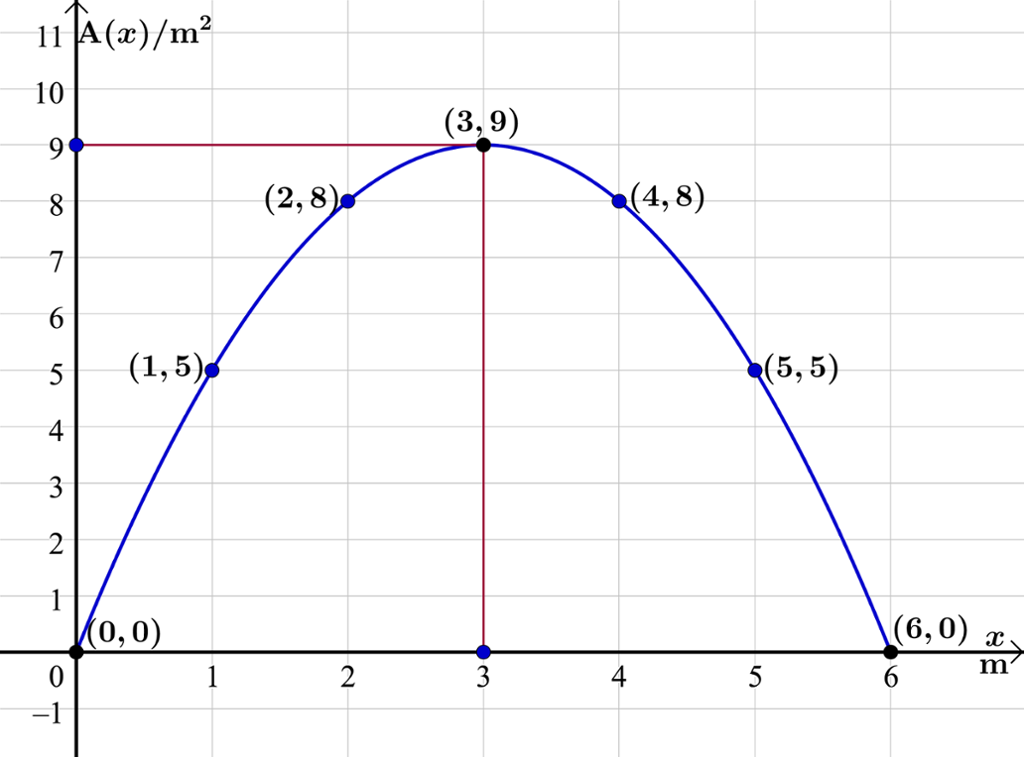
Vi har plottet punktene fra verditabellen i et koordinatsystem der førstekoordinaten er lengden på grunnlinja og andrekoordinaten er arealet til det tilhørende rektangelet.
Vi tegner grafen til funksjonen i samme koordinatsystem og ser at grafen går gjennom punktene som vi plottet fra verditabellen.
Grafen har et toppunkt, et punkt der funksjonen har sin maksimale verdi. Det vil si at det største arealet rektangelet kan få, er .
Nullpunktene finner vi der grafen skjærer førsteaksen, altså enten ved 0 eller 6 meter. Vi får da ikke noe reelt rektangel, og arealet blir 0.

Preikestolen er et fjellplatå i Rogaland som rager ca. 600 meter over Lysefjorden. Fjellveggen fra Preikestolen ned til fjorden er nesten loddrett.
Tenk deg at du står på kanten av Preikestolen og kaster en stein rett opp i lufta med utgangsfart . På nedturen passerer steinen på utsiden av platået og havner i Lysefjorden.
Naturens lover forteller oss at høyden til steinen er en funksjon av tida og er tilnærmet gitt med funksjonsuttrykket
Her står for tida i sekunder etter at steinen ble kastet.
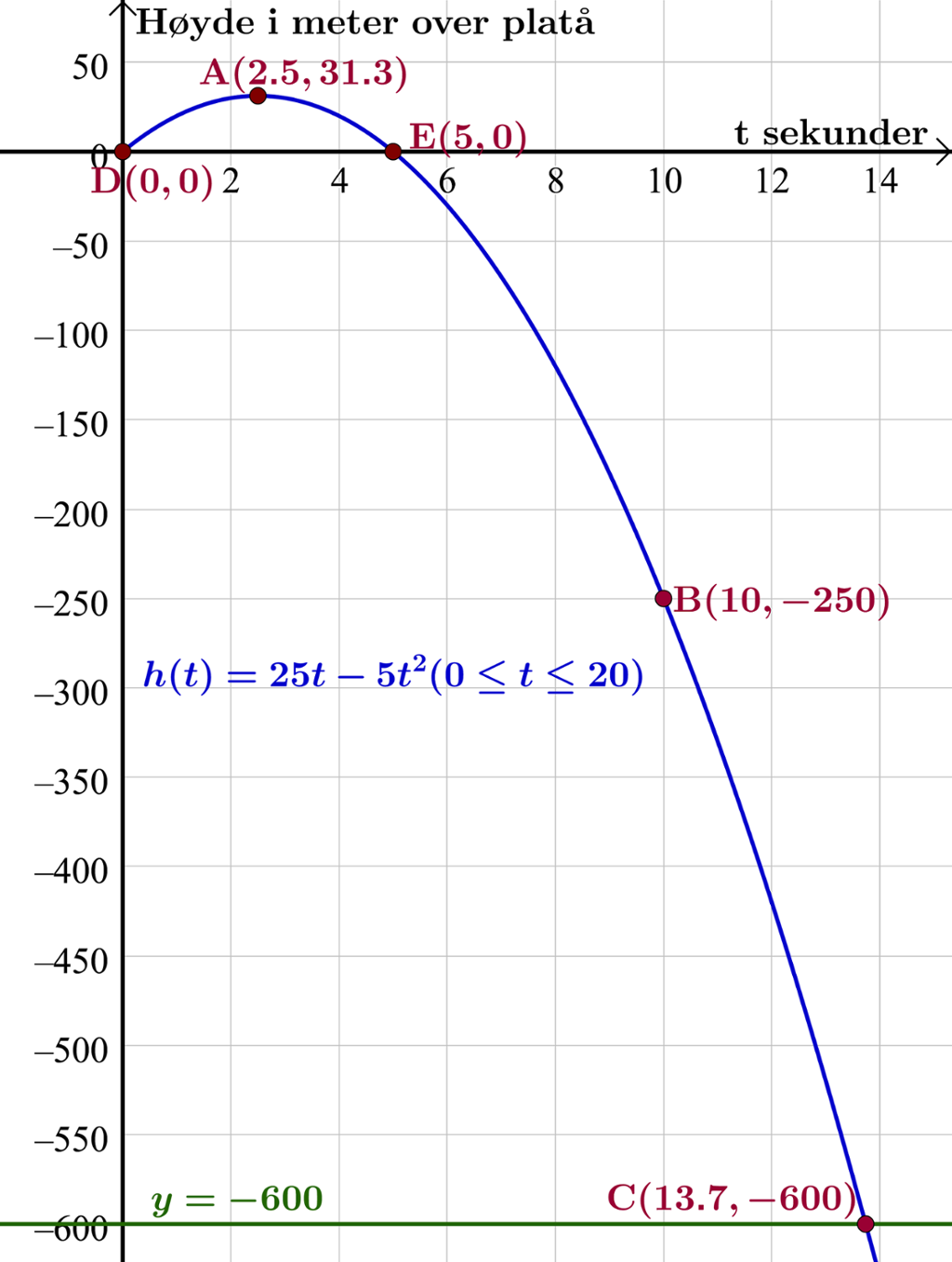
Høydefunksjonen er en andregradsfunksjon fordi variabelen er i andre potens.
Vi tegner grafen til funksjonen de første 20 sekundene ved å skrive h(t)=Funksjon[25t-5t^2, 0, 20].
Vi finner toppunktet, for eksempel ved kommandoen Ekstremalpunkt[h]. Det viser at steinen når sitt høyeste punkt 31,3 meter over platået etter 2,5 sekunder.
Vi finner punktet ved å skrive (10,h(10)). Det viser at steinen passerer 250 meter under platået etter 10 sekunder.
Vi tegner linja og finner skjæringspunktet mellom denne linja og grafen, for eksempel ved kommandoen Skjæring mellom to objekt. Vi får skjæringspunktet , som viser at steinen treffer Lysefjorden etter 13,7 sekunder.
Vi finner nullpunktene og , for eksempel ved kommandoen Nullpunkt[h]. Det viser at steinen forlater platået ved tida null og passerer platået på veien ned etter 5 sekunder.