Et praktisk eksempel på en tredjegradsfunksjon

Tenk deg at du skal lage en eske uten lokk av en kvadratisk papplate med sidelengder
60 cm. Du må da klippe bort et kvadrat i hvert hjørne av papplaten.
Du må altså klippe bort de fire mørkeblå kvadratene på tegningen nedenfor. De lyseblå rektangelene bretter du opp, og du får da en eske med det lyse kvadratet i midten som bunn.
Formen på esken avhenger av hvor store kvadrater du klipper bort. Vi kaller sidene i kvadratene du klipper bort for
Volumet av esken vil være avhengig av
Bunnen til esken blir et kvadrat med sider
Høyden på esken blir
Volumet er altså en polynomfunksjon av tredje grad. Vi ser også at
Hvis
Vi tegner nå grafen til volumfunksjonen.
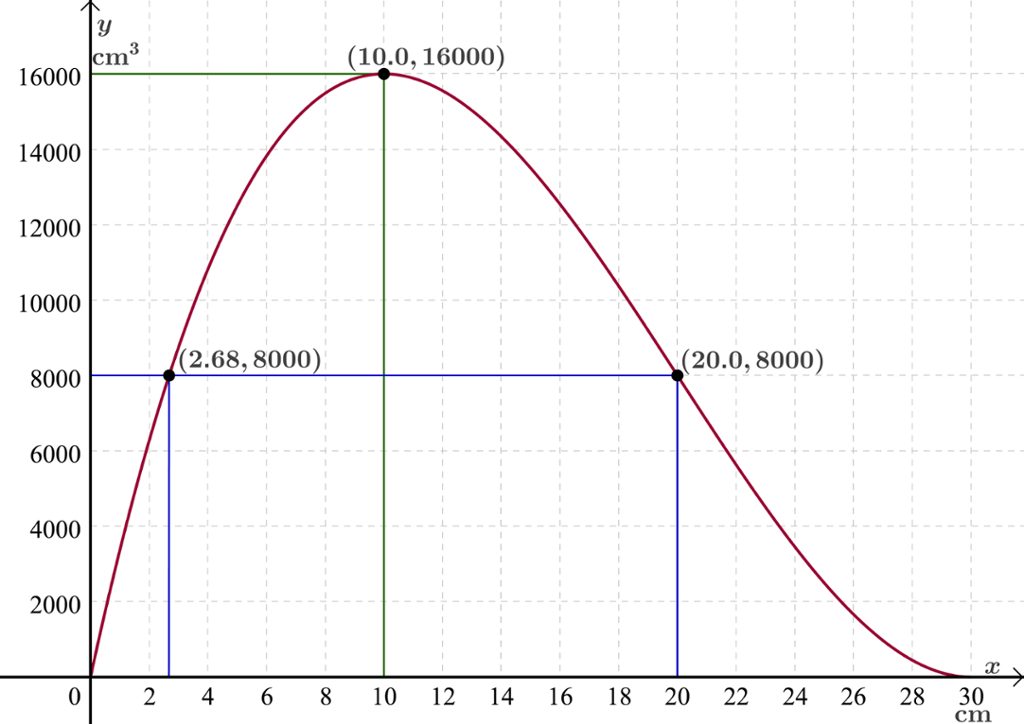
Vi ser av grafen at verdimengden er
Det vil si at volumet til esken er større enn
Vi kan ellers se av grafen at
- hvis vi ønsker en eske med størst mulig volum, må vi klippe bort kvadrater med sider
- hvis vi ønsker esker med volum lik
, må vi klippe bort kvadrater med sider eller - vi også kan gå motsatt vei og lese av hvor stort volum en bestemt verdi for
gir