Ulikheter av tredje grad

Vi skal løse ulikheten

Vi ordner ulikheten slik at vi får null på høyre side. Da kan vi faktorisere venstresiden, og ulikheten kan løses ved å studere fortegnet til det faktoriserte uttrykket.

Her har vi ikke noen informasjon som kan gi oss den første løsningen av likningen . Derfor må vi prøve oss fram, og vi finner at uttrykket blir null for .

Det viser at er en faktor i .

Vi utfører så polynomdivisjonen

Vi setter og finner nullpunktene

Vi har dermed nullpunktene , og .

Det betyr at

Ulikheten kan nå skrives slik

Vi tar nå «stikkprøver» innenfor hvert intervall for å finne ut hvilket fortegn uttrykket har i hvert av de fire intervallene .

For får vi

Uttrykket er negativt.

For får vi

Uttrykket er positivt.

For får vi

Uttrykket er negativt.

For får vi

Uttrykket er positivt.

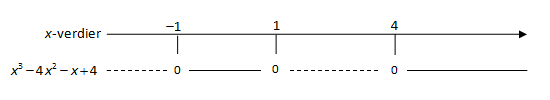
For å få en oversikt over situasjonen setter vi opp et fortegnsskjema. Vår oppgave var å finne ut for hvilke verdier av x det var slik at , det vil si at . Løsningen på oppgaven blir da at x må være mindre enn eller ligge mellom 1 og 4.

Løsningen er

Ved CAS i GeoGebra får vi

ø