Formlike trekanter
Figuren nedenfor viser to formlike trekanter. Som du ser, er to og to vinkler like store.
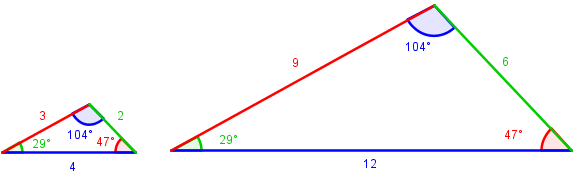
Den store trekanten er et forstørret bilde av den lille trekanten, og den lille trekanten er et forminsket bilde av den store trekanten.
Hvis vi kan vise at vinklene i to trekanter er parvis like store, har vi vist at trekantene er formlike.
Det er nok å vite at to par av vinkler i to trekanter er like store. På grunn av setningen om at summen av vinklene i en trekant alltid er lik grader, må nemlig også det tredje paret av vinkler være like store.
To sider som ligger «motsatt» av to vinkler som er like store, ligger på «tilsvarende» plasser i de to trekantene, og vi kaller dem for tilsvarende sider.
De blå sidene er tilsvarende fordi de ligger «motsatt» de blå vinklene som er like store.
De røde sidene er tilsvarende fordi de ligger «motsatt» de røde vinklene som er like store.
De grønne sidene er tilsvarende fordi de ligger «motsatt» de grønne vinklene som er like store.
Vi regner ut forholdet mellom lengdene av tilsvarende sider
Vi ser at forholdet er konstant lik . Vi kaller dette tallet for målestokken.
Sidene i den største trekanten er altså tre ganger så lange som sidene i den minste trekanten.
(Legg merke til at hvis vi ser på den lille trekanten som et bilde av den store trekanten, så er målestokken lik .)