Volum og overflate av kjegler og kuler

Volumet av en rett kjegle er av volumet av en rett sylinder med samme grunnflate og høyde.
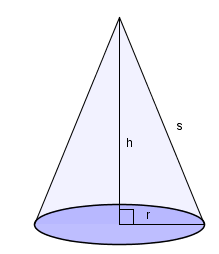
For å finne overflaten må vi tenke oss kjeglen klippet opp og lagt ut slik tegningen nedenfor viser.
Overflaten består av en sirkel, grunnflaten, og en sirkelsektor som er en del av en sirkel med radius
Buen i sirkelsektoren er lik omkretsen til grunnflaten.
Forholdet mellom arealet til sirkelsektoren og stor sirkel er lik forholdet mellom buelengden til sirkelsektoren og omkretsen til stor sirkel.
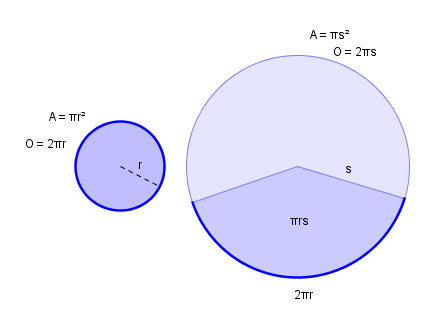
Formler for volum og overflate av en kjegle
Høyden
Eksempel
Regn ut volum og overflate av en kjegle der diameter i grunnflaten

Når vi skal regne ut overflaten, må vi finne arealet av sirkelsektoren med radius
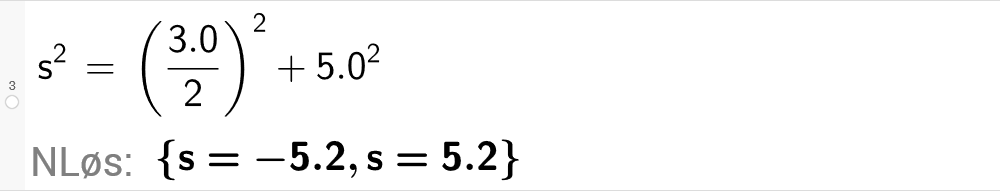
Vi finner sidekanten i kjeglen,

Vi kan finne volum og overflate av en kule ved å bruke formlene nedenfor.
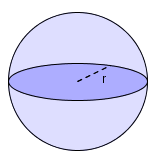
Volum og overfalte av en kule
Eksempel
Regn ut volumet og overflaten av en kule med radius

