Måleenheter for areal

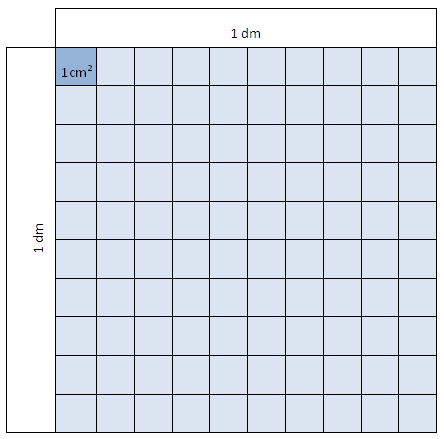
Vi definerer én kvadratdesimeter, 1 dm², som arealet, eller flateinnholdet, til et kvadrat med sidelengder på 1 dm.

Et kvadrat med sider 1 cm har et areal på én kvadratcentimeter, 1 cm².

Tilsvarende definerer vi arealer på 1 m², 1 mm² og så videre.

Figuren viser at det er 100 cm² i 1 dm². Det betyr igjen at

$1 {\mathrm{cm}}^2=\frac{1}{100}{\mathrm{dm}}^2=0,01 {\mathrm{dm}}^2$

På samme måte er det plass til 100 mm² i 1 cm² og 100 dm² i 1 m².

Akkurat som for lengde har det vært mange måleenheter for areal i bruk. Noen av dem bruker vi fortsatt, som for eksempel et dekar. Det kaller vi også et mål, og det blir brukt om tomtestørrelser. Et dekar tilsvarer 1 000 kvadratmeter. Dekar betyr 10 ar, og ar tilsvarer 100 kvadratmeter. En hektar er 10 dekar, eller 100 ar.

Vi husker sammenhengen mellom måleenheter for lengde og setter opp en tilsvarende tabell for arealsammenhengene:

På samme måte som med lengde trenger vi å kunne gjøre om mellom ulike enheter, men som vi så over, er det her plass til 100 cm² i 1 dm². Da må vi gange med eller dele på 100 når vi gjør om.

Eksempler

$$ \begin{array}{l}2,3{\mathrm{m}}^2=2,3·100{\mathrm{dm}}^2=230{\mathrm{dm}}^2\\ 2,3{\mathrm{m}}^2=2,3·{100}^2{\mathrm{cm}}^2=23 000{\mathrm{cm}}^2\\ 2,3{\mathrm{m}}^2=2,3·{10}^4{\mathrm{mm}}^2=2 300 000{\mathrm{mm}}^2\end{array}$$

$$ \begin{array}{l}4 500{\mathrm{cm}}^2=\frac{4 500}{100}{\mathrm{dm}}^2=45{\mathrm{dm}}^2\\ 4 500{\mathrm{cm}}^2=\frac{4 500}{{100}^2}{\mathrm{m}}^2=0,45{\mathrm{m}}^2\end{array}$$

Vi ser at det raskt blir ganske mange siffer.

Når vi setter opp måleenhetene for areal etter hverandre, som i tabellen nedenfor, kan vi ha som huskeregel at vi må gange med 100 når vi går én plass til høyre i tabellen (vi flytter kommaet to plasser til høyre), og vi må dele med 100 når vi går én plass til venstre (vi flytter kommaet to plasser til venstre).

Legg merke til at vi ikke har tatt med dekar i denne tabellen. Hvorfor har vi ikke det, tror du?

Også når vi jobber med areal, må vi ta hensyn til hvor presise målinger vi har gjort. Det er alltid den minst nøyaktige målingen som styrer hvor nøyaktig vi skal være i svaret. Vi ser på et eksempel der vi regner ut arealet av et rektangel.

Vi regner ut arealet på vanlig måte:

$$ 4,2 \mathrm{cm} · 5,75 \mathrm{cm} = 24,15 {\mathrm{cm}}^2$$

Når vi skal avgjøre hvor mye vi skal runde av, bruker vi som hovedregel like mange gjeldende siffer i svaret som i det måltallet med færrest gjeldende siffer. Vi definerer gjeldende siffer som alle siffer i tallet sett bort fra nuller først i tallet. Det betyr at 0,000 005 har ett gjeldende siffer, mens 500 000 har seks gjeldende siffer.

Det betyr at vi må runde av arealet vårt til 24 cm², siden høyden i rektangelet har kun to gjeldende siffer.

Det er vanlig å bruke minst to gjeldende siffer selv om ett av måltallene bare har ett siffer. Det er også sånn at svaret av og til får automatisk flere gjeldende siffer enn alle måltallene (prøv for eksempel å regne ut arealet av et kvadrat med sidelengde 20). Vi bruker sunn fornuft i praktiske eksempler. Reglene for bruk av gjeldende siffer er mye strengere i fag som for eksempel fysikk.

Når vi legger sammen ulike arealer, teller vi ikke gjeldende siffer, men ser på nøyaktigheten i målingene slik som når vi regner med lengder. En huskeregel er å bruke likt antall desimaler som det måltallet med færrest desimaler. Husk på at størrelsene må ha lik måleenhet!