Bokstavregning - Matematikk 1P-Y - TP - NDLA

Fagartikkel

Bokstavregning

Det er ofte lurt å regne med bokstaver i stedet for tall. Dette kalles algebra.

Bokstaver kan erstatte tall

Arealet av et rektangel

Et rektangel med påskriften g på en av de vannrette sidene og påskriften h på en av de loddrette sidene. Inni rektangelet står det A er lik g multiplisert med h. Illustrasjon. — Bilde: Bjarne Skurdal / CC BY-SA 4.0

Figuren viser et rektangel med grunnlinje g og høyde h. Formelen for å regne ut arealet av et rektangel er

$A = g \cdot h$

Du må altså multiplisere (gange) grunnlinja med høyden for å regne ut arealet.

Eksempel

Vi skal regne ut arealet til en fotballbane der sidelengdene er 68 m og 105 m.

En fotballbane er rektangelformet. Vi lar den lengste siden være grunnlinja og den korteste siden være høyden.

Fotballbane med tribuner. Foto. — Bilde: Vegard Grøtt / CC BY-NC-SA 4.0

Vi får at

$\begin{array}{rcl} A & = & g \cdot h \\ = & 105 m \cdot 68 m \\ = & 7 140 m^{2} \end{array}$

Bokstavene i formelen representerer tall, og en formel er en oppskrift for hvordan vi skal regne ut en størrelse ved å erstatte bokstavene med tall. Når vi kjenner grunnlinja og høyden, kan vi regne ut størrelsen arealet.

I mange tilfeller er det lurt å regne med bokstaver i stedet for tall. Dette kalles algebra.

Regnereglene vi bruker når vi regner med bokstaver, er akkurat de samme som gjelder for regning med tall. Hvis du lurer på om du har regnet riktig, kan du erstatte bokstavene med tall og se om utregningen gir samme svar.

Bokstaver og programmering

Vi kan lage et program som regner ut arealet av rektangler for oss. Når vi programmerer, lar vi ofte bokstaver, eller variabler, representere tall vi skal regne med. For eksempel kan vi i programmet lage en variabel h, la den stå for høyden i et rektangel og gi den verdien 68. I programmeringsspråket Python ville vi da ha skrevet

h = 68

Så kan vi lage en variabel "g" for grunnlinja i rektangelet og sette den til verdien 105 på tilsvarende måte. Til slutt kan vi be programmet regne ut arealet ved å skrive

g·h

i programmet.

Dette kan du lese mer om på teorisiden "Variabler, matematiske operatorer og kommandoen print()".

Regning med bokstaver

Vi kan regne med bokstaver uten å sette inn tall for dem, men vi må huske at bokstaver står for tall. Det vil si at vi må regne med bokstaver som om de var tall. Vi skal nå se på noen regler som forenkler regningen med bokstaver.

1. Vi sløyfer multiplikasjonstegnet mellom et tall og en bokstav

Når vi skriver produktet mellom to tall, for eksempel $2 \cdot 3$ , er multiplikasjonstegnet viktig. Uten multiplikasjonstegn ville det ha stått 23, som jo er noe ganske annet.

Når vi erstatter 3-tallet med en bokstav og får for eksempel $2 \cdot a$ , er det derimot vanlig å sløyfe multiplikasjonstegnet og bare skrive $2 a$ . Det vil si at $2 a$ betyr $2 \cdot a$ .

2. Vi kan forenkle uttrykk ved å addere og subtrahere like ledd

Vi tar for oss følgende regnestykke:

$2 \cdot 4 + 3 \cdot 4 = 8 + 12 = 20$

Siden både 2 og 3 skal ganges med 4, kan vi like gjerne regne slik:

$2 \cdot 4 + 3 \cdot 4 = (2 + 3) \cdot 4 = 5 \cdot 4 = 20$

Hvis vi nå erstatter tallet 4 med bokstaven $a$ , får vi

$2 \cdot a + 3 \cdot a = 2 a + 3 a = (2 + 3) a = 5 a$

Dette betyr at vi kan forenkle uttrykk ved å addere (legge sammen) og subtrahere (trekke fra) like ledd. For eksempel kan følgende uttrykk forenkles slik:

$\begin{matrix} 2 a + 3 b - 2 x + 7 & + 5 x - 2 - 7 b + 2 a \\ = 4 a - 4 b + 3 x + 5 \end{matrix}$

3. Vi forkorter brøker ved å dividere med samme faktor i teller og nevner

Når vi skal forkorte brøker, kan det være lurt å faktorisere først. For eksempel kan vi faktorisere tallet 6 til $2 \cdot 3$ . Tallene 2 og 3 er da faktorer i tallet 6.

Vi kan forenkle brøker ved først å faktorisere og så dividere (dele) med de samme faktorene i telleren og i nevneren (vi "stryker" faktor mot faktor):

$\frac{420}{30} = \frac{2 \cdot 2 \cdot 3 \cdot 5 \cdot 7}{2 \cdot 3 \cdot 5} = 14$

Hvis vi nå erstatter tallet 3 med bokstaven $a$ og tallet 5 med bokstaven $b$ , får vi tilsvarende:

$\frac{28 a b}{2 a b} = \frac{2 \cdot 2 \cdot a \cdot b \cdot 7}{2 \cdot a \cdot b} = 14$

4. Vi kan løse opp (fjerne) parenteser

Vi tar for oss dette regnestykket med tall:

$2 + (3 + 6 - 2) - (4 + 3 - 2)$

Fra reglene om regnerekkefølge har vi at det som står inni parenteser, alltid skal regnes ut først. Vi får derfor at

$2 + (3 + 6 - 2) - (4 + 3 - 2) = 2 + 7 - 5 = 4$

Men følgende måte å regne på gir det samme resultatet:

$2 + (3 + 6 - 2) - (4 + 3 - 2) = 2 + 3 + 6 - 2 - 4 - 3 + 2 = 4$

Husk at fortegnet til 3-tallet og 4-tallet inni parentesene egentlig er "+" (pluss) siden det ikke står noe fortegn. Med fortegn blir regnestykket slik:

$2 + (+ 3 + 6 - 2) - (+ 4 + 3 - 2) = 2 + 3 + 6 - 2 - 4 - 3 + 2 = 4$

Det viser seg at denne måten å regne på alltid blir riktig.

En parentes, inkludert regnetegnet pluss foran parentesen, kan fjernes ved at vi beholder alle leddene inni parentesen og oppfatter plusstegn og minustegn som regnetegn.

En parentes, inkludert regnetegnet minus foran parentesen, kan fjernes ved at vi skifter tegnene foran alle leddene inni parentesen og oppfatter disse som regnetegn.

Du kan lese om forskjellen på regnetegn og fortegn på teorisiden "Regnearter og negative tall".

5. Vi kan multiplisere tall med parentesuttrykk

Vi tar for oss regnestykket $10 \cdot (3 + 2)$ .

Siden det som står inni parentesen, skal regnes ut først, får vi at $10 \cdot (3 + 2) = 10 \cdot 5 = 50$ .

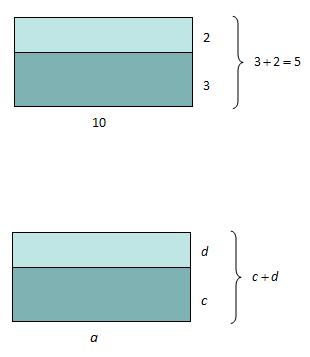
To like rektangler. Det første har grunnlinje lik 10 og høyde lik 5. Høyden er delt i 2 pluss 3 slik at rektangelet er delt i to deler med samme grunnlinje 10 og ulike høyder 2 og 3. Det andre rektangelet har grunnlinje lik a og høyde lik c pluss d. Høyden er delt i to deler slik at begge delene har grunnlinje a, men ulike høyder c og d. Illustrasjon.

Vi kan tolke dette geometrisk som arealet av hele det store rektangelet til høyre med grunnlinje 10 og høyde 5.

Dette arealet kan også betraktes som summen av arealene til de to små rektanglene. Disse er $10 \cdot 3$ og $10 \cdot 2$ .

Det betyr at

$10 \cdot (3 + 2) = 10 \cdot 3 + 10 \cdot 2$

Vi erstatter tallene i regnestykket ovenfor med bokstaver. Samme geometriske tolking på figuren til høyre som på figuren ovenfor gir at

$a \cdot (c + d) = a c + a d$

Generelt kan vi si at når vi multipliserer et tall med et parentesuttrykk, må vi multiplisere tallet med alle leddene inni parentesen, slik:

$a \cdot (c + d) = a c + a d$

Eksempel

$\begin{array}{rcl} 3 x (2 x^{2} - 4 x + 2) \\ = & 3 x \cdot 2 x^{2} - 3 x \cdot 4 x + 3 x \cdot 2 \\ = & 6 x^{3} - 12 x^{2} + 6 x \end{array}$

6. Vi kan multiplisere to parentesuttrykk med hverandre

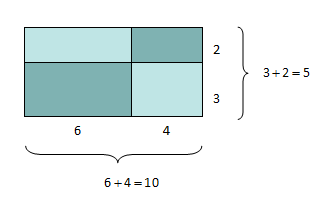
Et rektangel med grunnlinje 10 og høyde 5 som er delt i fire mindre rektangler. Dette er gjort ved å dele grunnlinja i 6 pluss 4 og høyden i 3 pluss 2. Illustrasjon.

Vi tar for oss regnestykket

$(6 + 4) \cdot (3 + 2)$

Siden det som står inni parentesen skal regnes ut først, får vi at

$(6 + 4) \cdot (3 + 2) = 10 \cdot 5 = 50$

Geometrisk kan vi tolke dette som arealet av hele det store rektangelet ovenfor med grunnlinje 10 og høyde 5.

Men vi ser geometrisk at dette arealet kan betraktes som summen av arealene av fire mindre rektangler. Disse arealene er henholdsvis $6 \cdot 3, 6 \cdot 2, 4 \cdot 3 og 4 \cdot 2$ .

Det betyr at

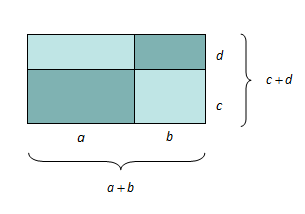
Et rektangel med grunnlinje a pluss b og høyde c pluss d som er delt i fire mindre rektangler. Dette er gjort ved å dele grunnlinja i a pluss b og høyden i c pluss d. Illustrasjon.

$\begin{array}{rcl} (6 + 4) \cdot (3 + 2) \\ = & 6 \cdot 3 + 6 \cdot 2 + 4 \cdot 3 + 4 \cdot 2 \end{array}$

Vi erstatter tallene i regnestykket ovenfor med bokstaver. Samme geometriske tolking på figuren til høyre som på figuren ovenfor gir at

$\begin{array}{rcl} (a + b) \cdot (c + d) \\ = & a c + a d + b c + b d \end{array}$

Generelt kan vi si at når vi multipliserer to parentesuttrykk med hverandre, må vi multiplisere hvert ledd i den ene parentesen med hvert ledd i den andre parentesen.

$(a + b) \cdot (c + d) = a c + a d + b c + b d$

Eksempel

$\begin{array}{rcl} (2 x - 4) \cdot (3 x + 2) \\ = & 2 x \cdot 3 x + 2 x \cdot 2 - 4 \cdot 3 x - 4 \cdot 2 \\ = & 6 x^{2} + 4 x - 12 x - 8 \\ = & 6 x^{2} - 8 x - 8 \end{array}$

Video om grunnleggende bokstavregning, del 1

Video: Olav Kristensen / CC BY-NC-SA 4.0

Video om grunnleggende bokstavregning, del 2

Kommer