Definisjon av bestemt integral som grenseverdi
Vi ser på funksjonen gitt ved
Nedenfor har vi tegnet grafen til i et koordinatsystem. Vi skal se hvordan vi kan finne arealet, , av det området som er farget blått.
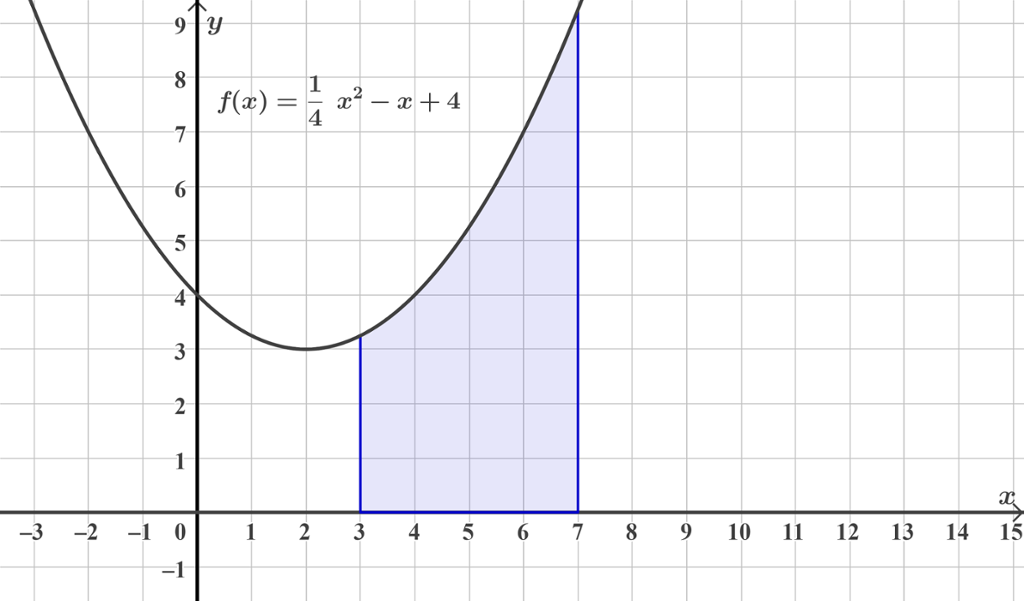
Det blå området er avgrenset av grafen til
I GeoGebra kan du legge inn funksjonen og få frem rektanglene med kommandoen SumUnder(f, 3, 7, 4). Tallene 3 og 7 er nedre og øvre grense langs
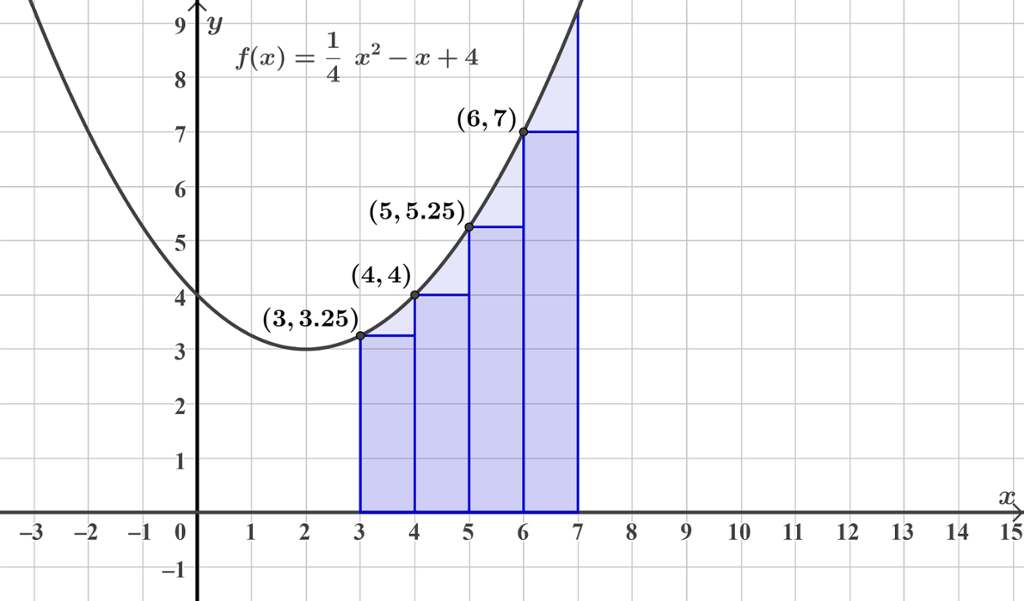
Vi ser at bredden av alle rektanglene i vårt tilfelle er 1, mens høyden varierer. Høyden er gitt ved funksjonsverdien for hver av
Vi kaller summen av de fire rektanglene for
Vi ser tydelig av figuren ovenfor at det samlede arealet av de fire rektanglene er mindre enn arealet av hele det blå området. Vi mangler de fire "nestentrekantene" mellom grafen og de fire rektanglene.
Men vi kan likevel si at
For å få en bedre tilnærming kan vi dele området i stadig flere rektangler. I GeoGebra kan du øke antall rektangler, det vil si at du øker det siste tallet i kommandoen SumUnder(). I det interaktive GeoGebra-arket nedenfor kan du endre antallet rektangler ved å dra i glideren. Hva skjer med arealet av alle rektanglene når antallet rektangler øker?
Vi ser at rektanglene dekker mer og mer av det blå området jo flere rektangler vi lager.
Vi tenker oss at vi fortsetter å øke antall rektangler "i det uendelige". Bredden til rektanglene, som vi kaller
Denne summen kaller vi for en Riemann-sum, oppkalt etter den tyske matematikeren Bernhard Riemann, som presenterte denne definisjonen i 1854.
Vi bruker den greske bokstaven
For å markere grenseverdien for denne summen når
Vi får da at arealet under grafen kan skrives som
Det er dette uttrykket som defineres som det bestemte integralet av
Det bestemte integralet fra
Geometrisk vil det bestemte integralet
En annen måte å finne en tilnærmet verdi for arealet TrapesSum(f, 3, 7, n), der verdien av
Hvis vi deler det området i fire trapeser, vil arealet av det første trapeset være gitt ved
Summen av arealene til de fire trapesene blir ut fra dette
Dette uttrykket kan forenkles slik:
Generelt kan vi si at trapesmetoden går ut på å gjøre en tilnærming av integralet