Rekker

Tenk deg at du får tilbud om å ta en sommerjobb. Arbeidsgiveren er litt rar og sier at du får 1 krone den første dagen du jobber. Så dobler han daglønna di for hver dag du er på jobb. Det vil si at du får 2 kroner den andre dagen du jobber, 4 kroner den tredje dagen og så videre.
Vi kan si at lønna di en bestemt dag, dag , er et ledd i en geometrisk følge der
Vi begynner med å finne samlet lønn den første uka, det vil si de 5 første arbeidsdagene. Da må vi regne ut summen av de fem første leddene i følgen:
Lønna den første uka blir på bare 31 kroner!
Men la oss finne ut hvor mye du vil tjene på 20 arbeidsdager med denne ordningen. Vi kunne selvsagt ha regnet ut hvert av de 20 leddene for hånd, men det slipper vi. Vi kan bruke ulike digitale hjelpemidler, her viser vi hvordan vi kan finne svaret ved hjelp av Python:
1lonn = 0 2dager = 20 3 4for n in range(1,dager + 1): 5 lonn = lonn + 2**(n-1) 6 7print("Samlet lønn blir", lonn, "kr.")
Kjør programmet og finn ut hva den samlede lønna blir etter 20 arbeidsdager.
Over har vi sett et eksempel på ei tallrekke, eller bare ei rekke. Ei slik rekke får vi når vi adderer leddene i en følge.
Leddene i ei rekke er de samme som i den tilsvarende følgen, og vi bruker de samme symbolene for leddene. Det første leddet kaller vi
På samme måte som vi skiller mellom endelige og uendelige følger, skiller vi mellom endelige og uendelige rekker.
Ei endelig rekke består av et endelig antall ledd slik som rekka vi så på over:
Ei uendelig rekke består av uendelig mange ledd slik som
Summen av de
Vi har en egen matematisk skrivemåte for summen av ei rekke. Da brukes den greske bokstaven stor sigma:
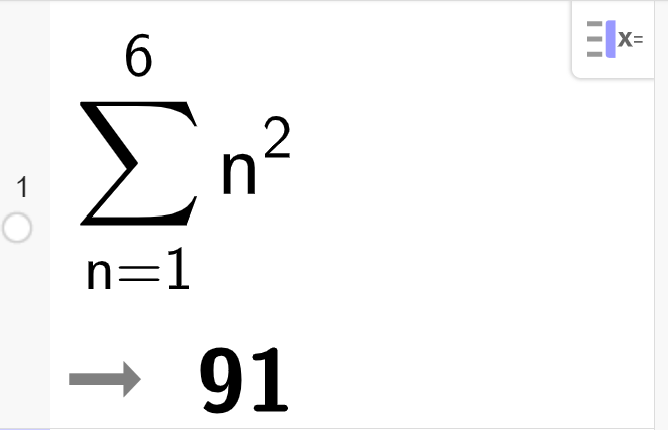
Vi kan regne ut summen av ei rekke hvis vi kjenner den eksplisitte formelen for Sum(n2,n,1,6):