Annuitetslån og nåverdier
Før eller siden får du kanskje behov for å låne penger. Det kan være penger for å kjøpe en bil eller kanskje en leilighet.
Et lån må tilbakebetales. I tillegg må det betales renter og gebyrer. Dette skjer ved at låntaker betaler et beløp et visst antall ganger, et visst antall terminer.
Hvis det betales et beløp hver måned, er det 12 terminer per år. Hvis det betales bare en gang per år, er det bare en termin per år. Det er også vanlig med for eksempel fire terminer per år. Da betales det et beløp hver tredje måned.
Antall terminer til sammen er lik antall terminer per år multiplisert med lånets løpetid i antall år. Løpetida er hvor lenge lånet varer, eller hvor lang tid det er fra du tar opp et lån til det er nedbetalt.
Terminbeløpet, det som betales en termin, består av en avdragsdel og en rentedel og kanskje et termingebyr. Avdragsdelen, eller avdraget, er den delen av terminbeløpet som går med til å betale ned på lånet. Rentedelen er det vi må betale for å få lov til å ha lånet. I tillegg kan det være et termingebyr, et fast beløp som skal betales.
Det skilles mellom to typer lån: serielån og annuitetslån. I denne artikkelen skal vi konsentrere oss om annuitetslån.
Den vanligste formen for lån er det vi kaller annuitetslån. Dette ordet kommer av det latinske ordet anno, som betyr "i året". Et slikt lån er kjennetegnet av at du betaler det samme beløpet hver gang gjennom hele perioden du skal betale tilbake lånet, altså at terminbeløpene er like store. Her vil vi operere med lån der du betaler ett avdrag i året. Dette gjør vi fordi utregningene ellers blir veldig komplekse. Vi vil heller ikke ta hensyn til eventuelle gebyrer.
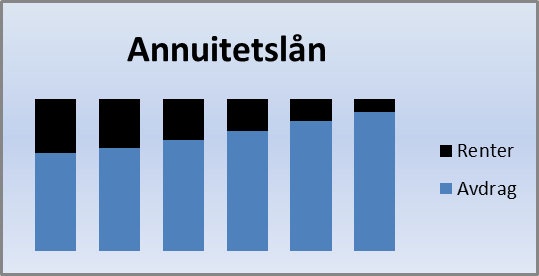
Etter hvert som lånet blir betalt ned, vil renteutgiftene bli mindre. Når terminbeløpet skal være like stort gjennom hele låneperioden, vil avdragsdelen øke når rentedelen går ned.
Når bankene skal beregne terminbeløpet for et annuitetslån, bruker de teorien om geometriske rekker.
Vi skal vise to ulike måter vi kan regne oss fram til terminbeløpene på, ut fra lånebeløp, rente og løpetid. I eksempelet vårt skal vi låne 200 000 kroner til ei årlig rente på 5 prosent. Løpetida skal være 10 år.
For å forstå hvordan bankene regner ut terminbeløpene, kan vi gjøre et tankeeksperiment. Vi forestiller oss at vi lar lånet stå og vokse i 10 år uten å betale inn noe på det. Hvor mye vil vi skylde banken etter 10 år?
Så tenker vi oss at vi i stedet for å betale inn penger til banken skal spare penger på en konto som også har 5 prosent rente. Det første beløpet setter vi inn om et år, det andre om to år og så videre. Det første beløpet vi setter inn, forrenter seg 9 ganger, mens det siste beløpet vi setter inn, ikke rekker å forrente seg i det hele tatt. Figuren under viser hvordan beløpene vi setter inn, forrenter seg gjennom de 10 årene:
Det vi betaler inn til sammen, er summen av alle uttrykkene som står i kolonnen til høyre:
Kan du finne
Hvis beløpet som står på kontoen etter 10 år, skal være nok til å betale ned hele lånet, må summen av denne rekka være lik summen vi skylder banken. Det gir denne likningen:

Denne løser vi enklest i CAS. Vi finner ut at terminbeløpet må være cirka 25 900 kroner for at lånet skal bli nedbetalt på 10 år.
I eksempelet over sammenlignet vi den framtidige verdien til lånebeløpet og terminbeløpene. Vi kan også regne omvendt, det vil si at vi regner om de framtidige innbetalingene til det vil kaller nåverdier. Da må vi huske på at det beløpet vi betaler inn, inneholder en del som er rente, og vi må dele på vekstfaktoren en gang per år akkurat denne delen av lånet har forrentet seg. Studer figuren under nøye. Hva blir
Vi legger sammen nåverdiene:
Vi ser at det første leddet i rekka,
En eksplisitt formel for rekka blir
Summen av nåverdiene til terminbeløpene må være lik det beløpet vi lånte, det gir denne likningen:
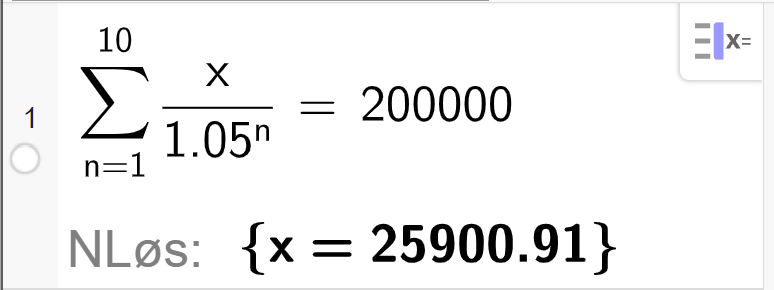
Vi løser likningen i GeoGebra:
Vi ser at løsningen heldigvis blir akkurat den samme som da vi sammenlignet framtidige verdier.