Stigningstall og konstantledd
Start med å lage to «glidere», og , i GeoGebra ved å skrive "" og "" i inntastingsfeltet.
Skriv så inn . Husk å skrive gangetegnet. Da skal du få en rett linje i grafikkfeltet slik som på bildet nedenfor.
Hva forteller og om grafen til en lineær funksjon
Du kan nå endre på verdiene til gliderne og samtidig se hvordan den rette linjen endrer seg.
Ser du noen sammenhenger mellom grafene og verdiene til og ?
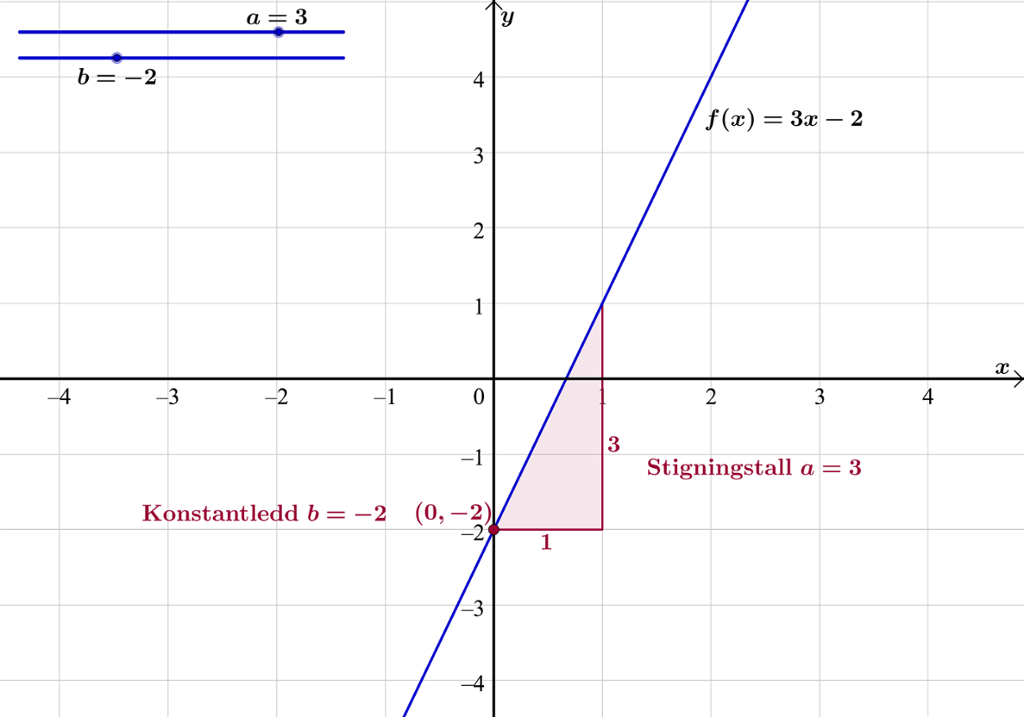
På bildet har vi tegnet grafen til for og
. Det betyr at .
Ser du at grafen skjærer -aksen der ? Grafen skjærer andreaksen når og
.
Tallet kalles konstantleddet.
Tallet viser hvor mye grafen stiger når øker med enhet.
Tallet kalles stigningstallet.
Hvis stigningstallet er negativt, synker grafen når øker.
Nedenfor har vi laget GeoGebra-arket du ble bedt om å lage øverst i teksten. Arket er interaktivt slik at du kan dra i gliderne for og og se hvordan den rette linjen endrer seg.
Prøv selv!
Dra i gliderne for og . Observer hva som skjer.
Oppgave
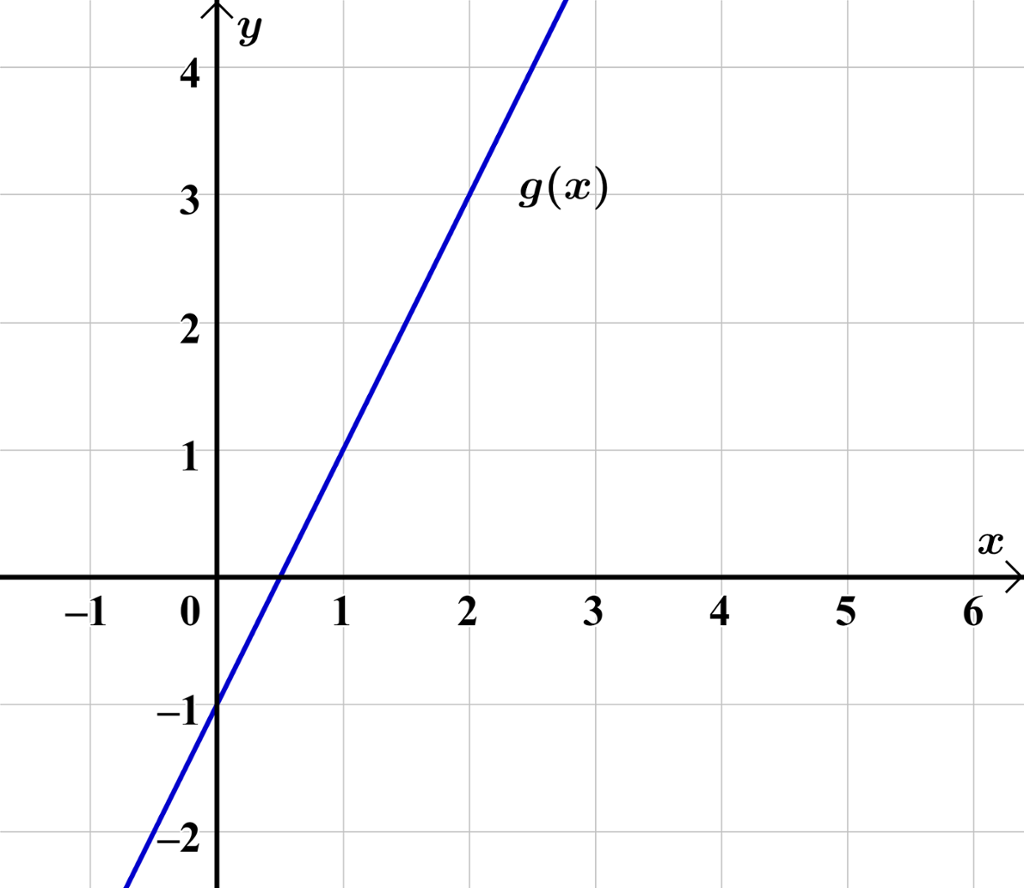
Finn funksjonsuttrykket til den lineære funksjonen på bildet ved å finne stigningstall og konstantledd.
Spesialtilfeller
Du bør merke deg to spesialtilfeller av lineære funksjoner.
Det ene er når . Da er , og og er proporsjonale størrelser. Tallet kalles i dette tilfellet proporsjonalitetskonstanten.
Det andre spesialtilfellet er når . Da er og grafen er parallell med -aksen.
Stigningstallet, , sier noe om hvor bratt grafen til den lineære funksjonen er.
Konstantleddet, , viser alltid hvor grafen skjærer andreaksen. Hvorfor er det slik?
