Å løse andregradslikninger med abc-formelen
Vi ser på den generelle andregradslikningen . Her får vi et lite problem ved at de samme bokstavene og er brukt både til å illustrere kvadratsetningen og andregradsuttrykket. Vi løser dette ved å bruke bokstavene og i kvadratsetningen slik at denne blir
Det er godt mulig at du kan komme fram til abc-formelen på egenhånd. Prøv deg uten å se på løsningen.
Tips: Bruk metoden med å danne fullstendig kvadrat.
Utledning av abc-formelen
abc-formelen
Andregradslikningen
Vi bruker tegnet
Når vi løser en andregradslikning med abc-formelen, ordner vi først likningen slik at den kommer på formen
Du husker kanskje at vi definerte kvadratroten bare til positive tall og null? Det vil si at andregradslikningen ikke har løsninger blant de reelle tallene når det som står under rottegnet, er mindre enn null. Kanskje det digitale verktøyet du bruker, da gir løsninger med bokstaven
Andregradslikningen har bare én løsning når det som står under rottegnet, er lik null.
Vi skal nå se på noen eksempler på bruk av abc-formelen.
Eksempel 1
Likningen har to løsninger. Det er altså to verdier for
Eksempel 2
Uttrykket under rottegnet er null, og vi får bare én løsning.
Eksempel 3
Vi får
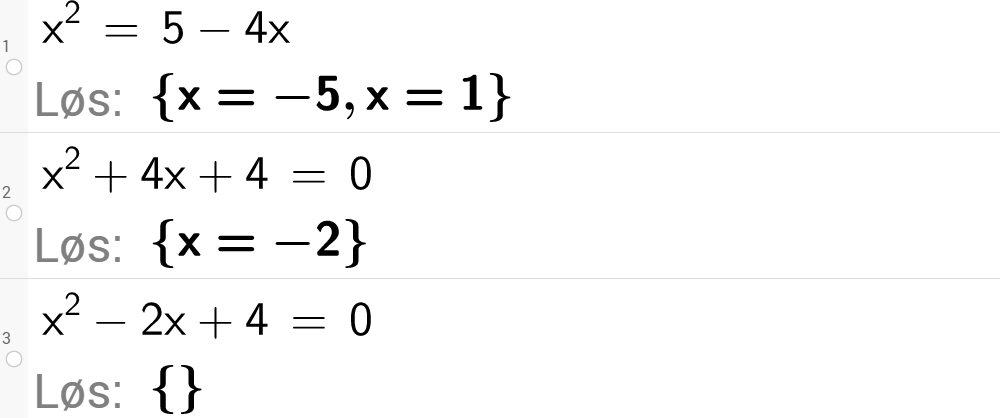
Ved CAS i GeoGebra får vi løsningene nedenfor ved å bruke knappen
Legg merke til markeringen for "ingen løsning" i linje 3.