Generelt om eksponentialfunksjoner

En funksjon $f$ på formen $f\left(x\right)=a·b^x$ kalles en eksponentialfunksjon. Tallet $b$ kalles vekstfaktoren.

Eksponentialfunksjoner er bare definert for positive verdier av $b$, og vi skal bare se på funksjoner der også $a$ er positiv.

Funksjonene $g$ og $h$ gitt nedenfor er eksempler på eksponentialfunksjoner.

Åpne bilde i et nytt vindu

CC BY-NC-SA

Bilde: Olav Kristensen, Stein Aanensen

$\begin{array}{rcl}g\left(x\right) & = & 2,5·1,5^x\\ & & \\ & & D_g=\left[-4, 6\right]\\ & & \\ h\left(x\right)& =& 6,5·0,8^x\\ & & \\ & & D_h=\left[-4, 6\right]\end{array}$

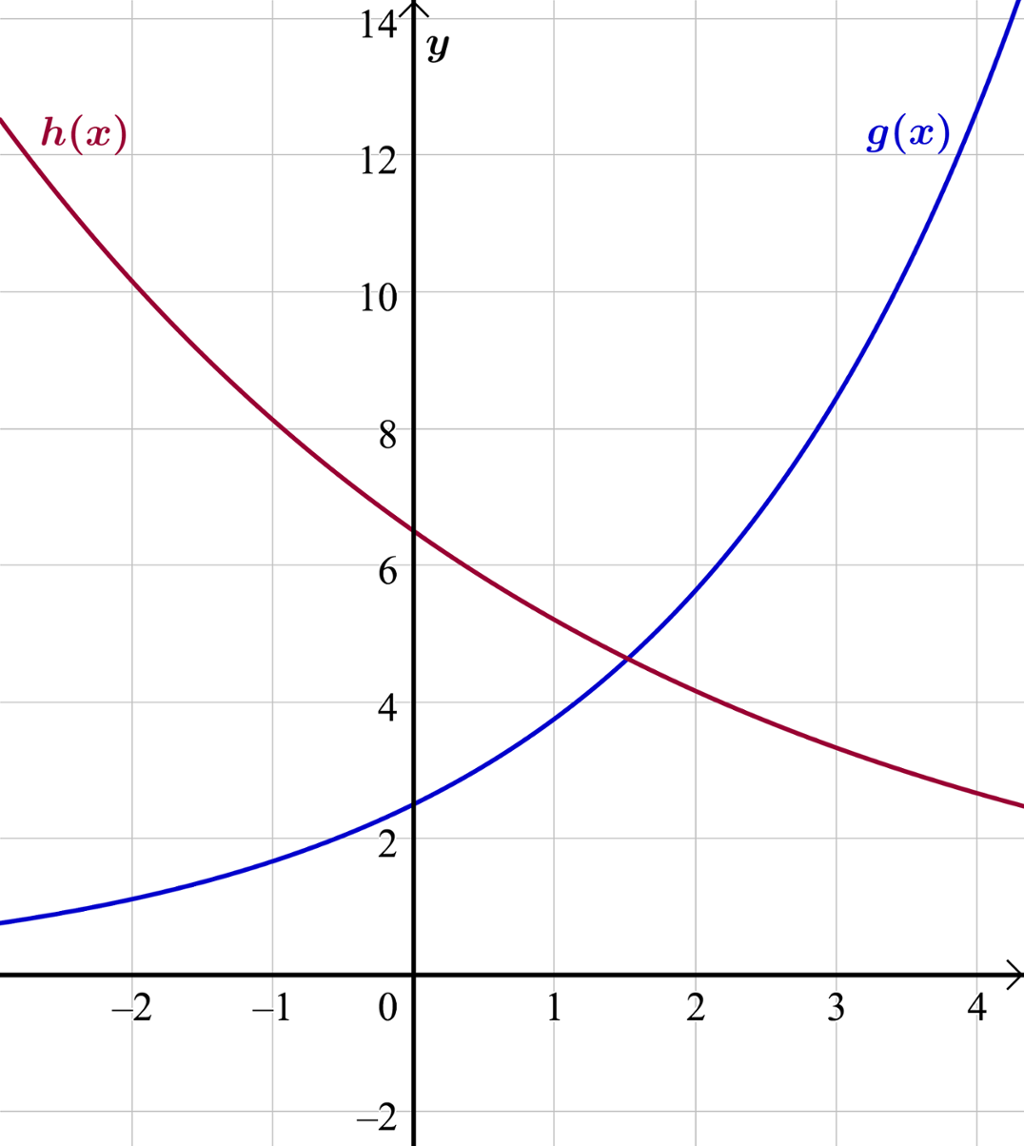
Når vekstfaktoren er større enn $1$, øker funksjonsverdiene med en fast prosent i like lange perioder. Sammenhengen mellom den prosentvise veksten $p$ og vekstfaktoren $b$ er gitt ved likningen

$b=1+\frac{p}{100}$

Når vekstfaktoren er mindre enn $1$, avtar funksjonsverdiene med en fast prosent i like lange perioder. Sammenhengen mellom den prosentvise nedgangen $p$ og vekstfaktoren $b$ er gitt ved likningen

$b=1-\frac{p}{100}$

Antall individer i en populasjon i naturen vil øke eksponentielt hvis populasjonen har ubegrenset tilgang til mat og ingen fiender. Populasjonen vil ikke vokse så fort i begynnelsen, men etter hvert vil veksten øke mer og mer. Dette er karakteristisk for eksponentiell vekst (se grafen til $g$ i koordinatsystemet).

Vi vil også få eksponentiell vekst på et bankinnskudd med en fast årlig rente.

Verdien på en gjenstand, for eksempel en bil, vil ofte utvikle seg som en eksponentialfunksjon med vekstfaktor mindre enn 1. En slik funksjon vil ha form som funksjonen $h$, se koordinatsystemet.