Tierpotenser og tall på standardform
Vi bruker ofte potenser med grunntallet 10 når vi regner svært store tall eller svært små tall. Tabellen nedenfor viser tierpotenser av ulik størrelse. Disse har egne navn (prefikser). En del av disse bør du kunne.
En oversikt over noen prefiks til tierpotenser:
Prefiks | Symbol | Navn |
| |
|---|---|---|---|---|
1015 | peta | P | billiard | 1 000 000 000 000 000 |
1012 | tera | T | billion | 1 000 000 000 000 |
109 | giga | G | milliard | 1 000 000 000 |
106 | mega | M | million | 1 000 000 |
103 | kilo | k | tusen | 1000 |
102 | hekto | h | hundre | 100 |
101 | deka | da | ti | 10 |
10-1 | desi | d | tidel | 0,1 |
10-2 | centi | c | hundredel | 0,01 |
10-3 | milli | m | tusendel | 0,001 |
10-6 | mikro | μ | milliondel | 0,000 001 |
10-9 | nano | n | milliarddel | 0,000 000 001 |
Prefikser
Kilo er opprinnelig et gresk ord som betyr tusen. Vi bruker ordet ved å sette det foran for eksempel meter og får da en større lengde, nemlig kilometer. Vi bruker også symbolet k for kilo, og skriver da kilometer kortfattet som km. Et ord som på denne måten settes foran et annet ord, kalles for et prefiks.
Markedsverdien av oljefondet kan det være interessant å følge med på. Høsten 2020 kunne denne verdien variere mellom 10 680 milliarder kroner og 10 710 milliarder kroner i løpet av bare fem minutter.
Det er ikke noe poeng for oss å vite på kronenivå hva verdien er. Det holder for oss å avrunde verdien til cirka 11 000 milliarder kroner.
Det er også greit å skrive tall kun med tallsifre. For eksempel har ordet billion ulik betydning i Norge og i USA. 11 000 milliarder kroner blir da 11 000 000 000 000 kroner. Det blir svært mange sifre å holde styr på.
11 000 000 000 000 kan også skrives som . Da har vi skrevet tallet på standardform.
Definisjon av standardform
Et tall er skrevet på standardform når det skrives som et tall fra 1 til 10 multiplisert med en potens av 10 der eksponenten er et helt tall.
Et tall er skrevet på standardform når det er skrevet på formen
Hvorfor og hvordan vi kan skrive tall på standardform
Vi ser på tallet 2 357. Tallsystemet vårt er et posisjonssystem. Det vil si at det er det enkelte siffers plassering som bestemmer verdien til sifferet.
Det første sifferet, 2, har verdien 2 000. Det neste, 3, har verdien 300. Sifferet 5 har verdien 50, mens det siste sifferet, 7, forteller at vi har 7 enere. Det første sifferet angir altså antall 1 000, det neste antall 100, det tredje antall tiere og det siste antall enere.
Vi kan sette et kommategn etter sifferet 7. Da vil eventuelle sifre etter 7 angi antall tideler, hundredeler og så videre avhengig av sifferets posisjon.
Kommategnet forteller altså hvor vi begynner å telle enere.
Vi kan flytte kommaet en plass til venstre og skrive
Vi kan fortsette slik:
I den siste linja har vi skrevet tallet 2 357 som et tall mellom 1 og 10 multiplisert med en tierpotens. Vi sier da at vi har skrevet tallet på standardform.
I begynnelsen av 2011 var folketallet i verden cirka 6 894 000 000.
Dette tallet kan vi skrive på standardform som
Ovenfor har vi avrundet til én desimal i desimaldelen av tallet. Vi må da huske på de reglene som gjelder for avrunding.
Avrunding
Når vi avrunder et desimaltall, må vi se på den desimalen som kommer nærmest etter den siste vi beholder. Hvis denne desimalen er 5 eller høyere, må vi øke den siste desimalen vi beholder, med 1.
Små tall på standardform
Vi ser på tallet
Vi kan flytte kommaet en plass til høyre og skrive
I den siste linja har vi skrevet tallet
Husk definisjonen:
Vann er bygd opp av vannmolekyler. Massen til ett vannmolekyl er
Her ser du at det er hensiktsmessig å bruke standardform.
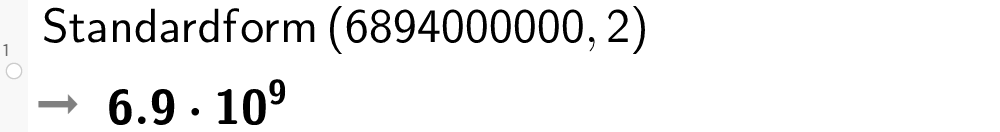
I GeoGebra bruker vi kommandoen "Standardform(<Tall>)" eller "Standardform(<Tall>,<Gjeldende siffer>)" for å skrive et tall eller regneuttrykk på standardform.

I GeoGebra benyttes også bokstaven E for tierpotens.