Fagartikkel

Mer om forenkling av rasjonale uttrykk

Hvordan skal vi trekke sammen (addere og subtrahere) rasjonale uttrykk som også inneholder andregradsuttrykk?

Gjennom tre eksempler skal vi illustrere hvordan vi ved hjelp av reglene for brøkregning og faktoriseringsreglene kan trekke sammen og forenkle rasjonale uttrykk som også inneholder andregradsuttrykk. Nederst finner du hvordan vi løser oppgavene med CAS i GeoGebra.

Husker du at et tall som kan skrives som en brøk med hele tall i teller og nevner, kalles et rasjonalt tall? På samme måte er et typisk rasjonalt uttrykk en brøk med bokstavuttrykk i teller og nevner.

Eksempel 1

Vi skal forkorte brøken

$\frac{x^{2} - 5 x + 6}{x - 3}$

Først faktoriserer vi telleren $x^{2} - 5 x + 6$ ved stirremetoden. Da må vi finne to tall hvis produkt er lik 6 og sum er lik $- 5$ . Tallene $- 2 og - 3$ oppfyller disse kravene. Det betyr at

$x^{2} - 5 x + 6 = (x - 2) (x - 3)$ .

Da er

$\frac{x^{2} - 5 x + 6}{x - 3} = \frac{(x - 2) (x - 3)}{x - 3} = x - 2$

Eksempel 2

Vi skal forkorte brøken

$\frac{x^{2} + 3 x + 2}{2 x + 2}$

Først faktoriserer vi telleren $x^{2} + 3 x + 2$ ved stirremetoden. Da må vi finne to tall hvis produkt er lik 2 og sum er lik 3. Tallene 1 og 2 oppfyller disse kravene. Det betyr at

$x^{2} + 3 x + 2 = (x + 1) (x + 2)$

Da er

$\frac{x^{2} + 3 x + 2}{2 x + 2} = \frac{(x + 1) (x + 2)}{2 (x + 1)} = \frac{x + 2}{2}$

Eksempel 3

Vi skal trekke sammen og forkorte

$\frac{1}{2 x - 2} + \frac{2}{x - 3} - \frac{x - 2}{x^{2} - 4 x + 3}$

Først faktoriserer vi nevnerne. Vi starter med å finne nullpunktene til nevneren $x^{2} - 4 x + 3$ .

$\begin{array}{rcl} x^{2} - 4 x + 3 & = & 0 \\ x & = & \frac{- (- 4) \pm \sqrt{{(- 4)}^{2} - 4 \cdot 1 \cdot 3}}{2 \cdot 1} \\ x & = & \frac{4 \pm 2}{2} \\ x_{1} & = & 1 x_{2} = 3 \end{array}$

Nevneren i den tredje brøken har altså nullpunktene $x = 1 og x = 3$ .

Det gir at $x^{2} - 4 x + 3 = (x - 1) (x - 3)$ .

Nevneren i den første brøken faktoriserer vi slik:

$2 x - 2 = 2 (x - 1)$

Det betyr at fellesnevneren for de tre nevnerne er

$2 (x - 1) (x - 3)$

Da er

$\begin{array}{rcl} \frac{1}{2 x - 2} & + & \frac{2}{x - 3} - \frac{x - 2}{x^{2} - 4 x + 3} \\ = & \frac{1}{2 (x - 1)} + \frac{2}{(x - 3)} - \frac{x - 2}{(x - 1) (x - 3)} \\ = & \frac{1 \cdot (x - 3)}{2 (x - 1) \cdot (x - 3)} + \frac{2 \cdot 2 (x - 1)}{(x - 3) \cdot 2 (x - 1)} - \frac{(x - 2) \cdot 2}{(x - 1) (x - 3) \cdot 2} \\ = & \frac{x - 3}{2 (x - 1) (x - 3)} + \frac{4 x - 4}{2 (x - 1) (x - 3)} - \frac{(2 x - 4)}{2 (x - 1) (x - 3)} \\ = & \frac{x - 3 + 4 x - 4 - (2 x - 4)}{2 (x - 1) (x - 3)} \\ = & \frac{x - 3 + 4 x - 4 - 2 x + 4}{2 (x - 1) (x - 3)} Husk å skifte fortegn! \\ = & \frac{3 x - 3}{2 (x - 1) (x - 3)} \\ = & \frac{3 (x - 1)}{2 (x - 1) (x - 3)} \\ = & \frac{3}{2 (x - 3)} \end{array}$

Brøker som utvides og forkortes endrer ikke verdi.

Når en brøk utvides, multipliseres teller og nevner med samme tall. Brøken endrer ikke verdi.
Når en brøk forkortes, divideres teller og nevner med samme tall. Brøken endrer ikke verdi.

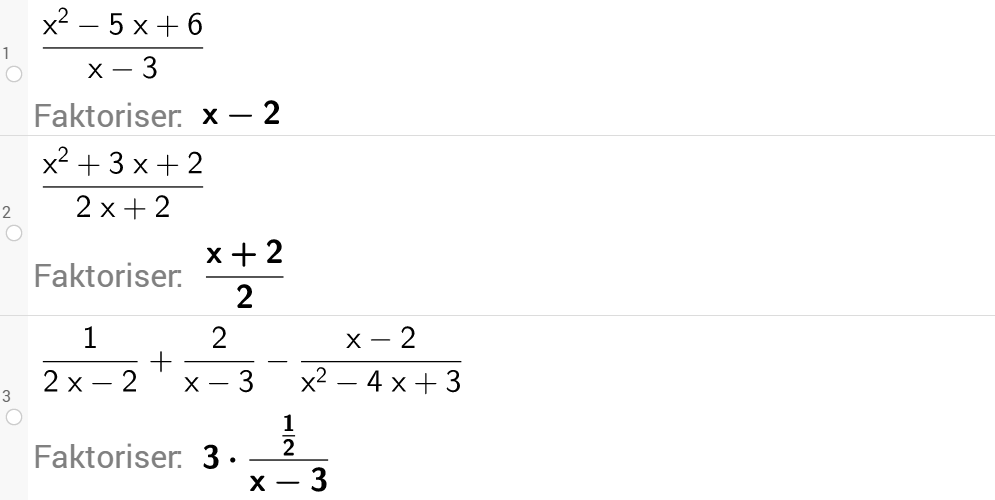
Faktorisering av rasjonale uttrykk i GeoGebra. Skjermdump. — Bilde: Olav Kristensen / CC BY-NC-SA 4.0

Ved CAS i GeoGebra får vi de samme løsningene som i eksemplene over ved å bruke faktoriseringskommandoen.

Video: Tom Jarle Christiansen / CC BY-SA 4.0