Likningssett med andregradslikninger

På teorisiden "Likningssett" løser vi likningssett med to likninger av første grad. Et likningssett kan inneholde alle typer likninger, og oftest er det enkleste å løse likningssettene med et digitalt hjelpemiddel, slik vi viser lenger ned på siden. Men vi kan også løse slike for hånd.

Når vi løser likningssett med to likninger av første grad, bruker vi blant annet innsettingsmetoden. Denne metoden kan vi også bruke her. Dersom den ene likningen er av første grad, er ofte det lureste å finne et uttrykk for den ene ukjente ved hjelp av førstegradslikningen, og så sette dette uttrykket inn i andregradslikningen.

Eksempel

Vi har gitt likningssettet

$\left[\begin{array}{c}2x^2-2x-y^2=8\\ 2x-y=-2\end{array}\right]$

Vi bruker førstegradslikningen til å finne et uttrykk for $y$:

$$ \begin{array}{rcl}2x-y& = & -2\\ -y& =& -2-2x\\ y& =& 2x+2\end{array}$$

Vi setter så uttrykket for $y$ inn i andregradslikningen:

$$ \begin{array}{rcl}2x^2-2x-y^2& = & 8\\ 2x^2-2x-{\left(2x+2\right)}^2& =& 8\\ 2x^2-2x-\left(4x^2+8x+4\right)& =& 8\\ 2x^2-2x-4x^2-8x-4& =& 8\\ -2x^2-10x-12& =& 0 \overline{):-2}\\ x^2+5x+6& =& 0\\ \left(x+2\right)\left(x+3\right)& =& 0\\ & & \\ x+2=0& \vee & x+3=0\\ x=-2& \vee & x=-3\end{array}$$

Vi setter så disse løsningene inn i uttrykket for y:

$$ \begin{array}{rcl}y& = & 2x+2\\ & & \\ y& =& 2·(-2)+2=-2\\ & \vee & \\ y& =& 2·(-3)+2=-4\end{array}$$

Likningssettet har to sett med løsninger:

$x=-2 \wedge y=-2 \vee x=-3 \wedge y=-4$

🤔 Tenk over: Hvor mange sett med løsninger har et likningssett som inneholder én andregradslikning?

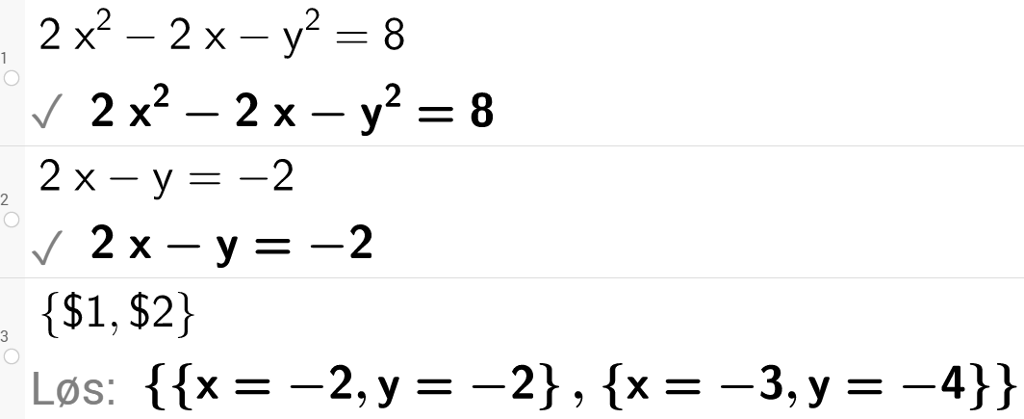
Løsning med CAS

Vi kan løse likningssettet i GeoGebra.

Vi markerer rutene der likningene våre står (her 1 og 2), for deretter å bruke $$ \boxed{\mathrm{x}\underset{}{\overset{\stackrel{}{}}{\mathbf{=}}}}$$ .

Du kan også bruke kommandoen Løs({likning, likning},{x,y}) for å løse likningen.