Å finne en ukjent side i en rettvinklet trekant

Hvor lang er siden på figuren?
Løsning
Siden
Siden
Hvor lang er siden
Løsning
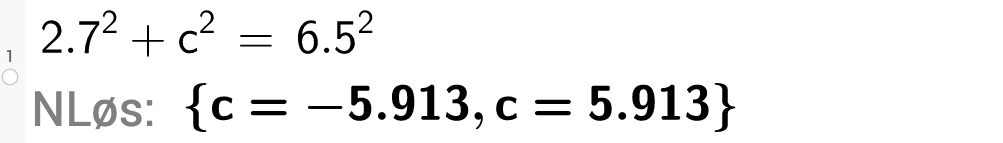
Pytagoras' setning gir
Siden
En stige skal plasseres
Hvor lang må stigen være?
Løsning
La stigen være
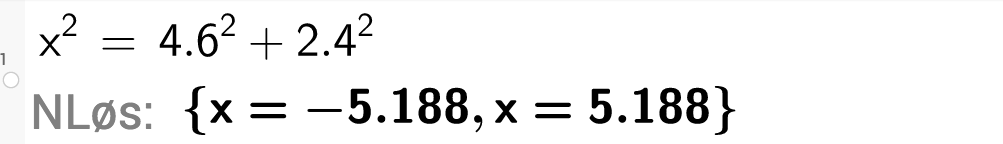
Pytagoras' setning gir
Stigen må være
Noen ganger bruker vi Pytagoras' setning for å lage vinkler som er 90 grader.
Snekker Pettersen skulle bygge en garasje. Det var svært viktig at alle hjørnene ble rette vinkler.
Vinkelmåleren han brukte til vanlig ble litt for liten, slik at den ga unøyaktig vinkel. Pettersen saget da til to bordlengder, den ene på 3 m, og den andre på 4 m. Han festet bordlengdene i endene som vist på tegningen, og la dem slik at avstanden mellom de røde punktene ble 5 m. Han brukte til slutt en tredje bordlengde og spikret det sammen.
Pettersen brukte Pytagoras' setning for å lage seg en rett vinkel. Her er en video som viser bruk av de samme sidelengdene til å lage seg en rett vinkel.
Mål lengde, bredde og diagonal til pulten eller bordplata du jobber ved.
Kvadrer alle lengdene. Sjekk om summen av kvadratene til lengde og bredde er lik kvadratet til hypotenusen. Hvis ikke, så er bordplata skeiv.